Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Nhân phương trình thứ nhất với -3 rồi cộng vào phương trình thứ hai.
Lại nhân phương trình thứ nhất rồi cộng vào phương trình thứ ba thì được hệ:
(I) ⇔ (II)
⎧⎪⎨⎪⎩x+3y+2z=1−4y−7z=6−17y−13z=−8{x+3y+2z=1−4y−7z=6−17y−13z=−8
Nhân phương trình thứ hai của hệ (II) với 17 rồi cộng vào phương trình thứ ba thì được:
(II) ⇔ (III)
⎧⎪⎨⎪⎩x+3y+2z=1−4y−7z=6−67z=134{x+3y+2z=1−4y−7z=6−67z=134
Hệ phương trình (III) có dạng tam giác. Tìm giá trị các ẩn ngược từ dưới lên dễ dàng tìm được nghiệm của hệ phương trình đã cho:
(x, y, z) = (-1, 2, -2)


\(b,ĐK:-\dfrac{1}{3}\le x\le2\\ PT\Leftrightarrow3x+1=4x^2-16x+16\\ \Leftrightarrow4x^2-19x+15=0\\ \Leftrightarrow\left[{}\begin{matrix}x=\dfrac{15}{4}\left(ktm\right)\\x=1\left(tm\right)\end{matrix}\right.\Leftrightarrow x=1\\ d,\Leftrightarrow\left\{{}\begin{matrix}x=5-3y\left(1\right)\\\left(5-3y\right)^2+2y^2=25\left(2\right)\end{matrix}\right.\\ \left(2\right)\Leftrightarrow11y^2-30y=0\\ \Leftrightarrow y\left(11y-30\right)=0\Leftrightarrow\left[{}\begin{matrix}y=0\Rightarrow x=5-3\cdot0=5\\y=\dfrac{30}{11}\Rightarrow y=5-3\cdot\dfrac{30}{11}=-\dfrac{35}{11}\end{matrix}\right.\)
Vậy \(\left(x;y\right)\in\left\{\left(5;0\right);\left(-\dfrac{35}{11};\dfrac{30}{11}\right)\right\}\)

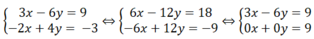
⇒ hệ phương trình vô nghiệm do phương trình 0x + 0y = 9 vô nghiệm.
Nhận xét: Hệ phương trình trên vô nghiệm.
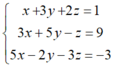

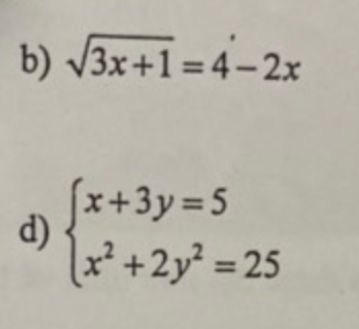

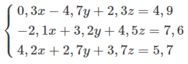
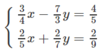
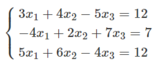
Nhân phương trình (2) với 2 rồi cộng với phương trình (1) và nhân phương trình (2) với 3 rồi trừ đi phương trình (3), phương trình (2) giữ nguyên ta được:
Giải hệ phương trình trên ta được x = -1; y = 2; z = -2.
Vậy hệ phương trình có nghiệm (x; y; z) = (-1; 2; -2)