
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có: 2 x y + y 2 − 4 x − 3 y + 2 = 0 x y + 3 y 2 − 2 x − 14 y + 16 = 0 ⇒ 2 x y + y 2 − 4 x − 3 y + 2 = 0 2 x y + 6 y 2 − 4 x − 28 y + 32 = 0
⇒ 5 y 2 − 25 y + 30 = 0 ⇒ y = 3 ; y = 2
Khi y = 3 thì phương trình đầu trở thành 6 x + 9 - 4 x - 9 + 2 = 0 ⇔ x = - 1
Khi y = 2 thì phương trình đầu trở thành 4 x + 4 - 4 x - 6 + 2 = 0
⇔ 0 x = 0 ⇔ x ∈ R
Đáp án cần chọn là: A

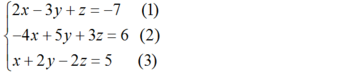
Đưa hệ phương trình về hệ dạng tam giác bằng cách khử dần các ẩn.
Nhân phương trình (1) với 2 rồi cộng với phương trình (2) và nhân phương trình (3) với 4 rồi cộng với phương trình (2) ta được:
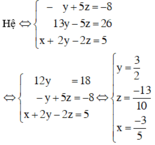
Vậy hệ phương trình có nghiệm 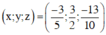

Ta có: \(\left\{{}\begin{matrix}x^4+2x^3y+x^2y^2=2x+9\\x^2+2xy=6x+6\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}\left(x^2+xy\right)^2=2x+9\\x^2+2xy=6x+6\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left(x^2+xy\right)^2=2x+9\\xy=3x+3-\dfrac{x^2}{2}\end{matrix}\right.\) \(\Rightarrow\left(\dfrac{x^2}{2}+3x+3\right)^2=2x+9\)( đến đây là phương trình 1 ẩn rồi, tự giải tiếp)

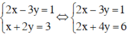 (Nhân cả hai vế phương trình thứ hai với 2)
(Nhân cả hai vế phương trình thứ hai với 2)
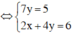 (Lấy phương trình thứ hai trừ đi phương trình thứ nhất).
(Lấy phương trình thứ hai trừ đi phương trình thứ nhất).
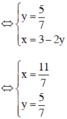
Vậy hệ phương trình có nghiệm 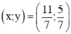

Bất phương trình bậc nhất 2 ẩn :
\(2x+3y>0\Rightarrow Câu\) \(C\)
\(x-2y\le1\Rightarrow Câu\) \(f\)
\(4\left(x-1\right)+5\left(y-3\right)>2x-9\)
\(\Leftrightarrow4x-4+5y-15-2x+9>0\)
\(\Leftrightarrow2x+5y-10>0\) \(\Rightarrow Câu\) \(i\)
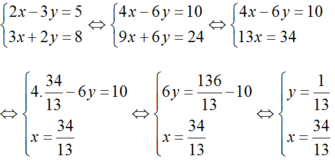
từ pt trên tính x theo y hoặc y theo x r thay vào pt dưới