Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

b: ΔOBA vuông tại B có BI là đường cao
nên OI*IA=BI^2
=>OI*OA=1/4BC^2
Xét ΔABD và ΔAEB có
góc ABD=góc AEB
góc BAD chung
=>ΔABD đồng dạng với ΔAEB
=>AB/AE=AD/AB
=>AE*AD=AB^2=AB*AC



I - Trắc nghiệm khách quan (4 điểm)
Khoanh tròn vào chữ A hoặc B, C, D trước phương án chọn đúng.
Câu 1. Trong các công thức hoá học sau, công thức hoá học của chất hữu cơ là
A. CO2. B. Na2CO3. C. CO. D. CH3Cl.
Câu 2. Đốt cháy 32g khí mêtan, thể tích CO2 sinh ra (ở đktc) là
A. 11,2 lít. B. 22,4 lít. C. 33,6 lít. D. 44,8 lít.
Câu 3. Etilen không tác dụng với chất nào sau đây?
A. CH4 B. Br2 C. H2 D. O2
Câu 4. 14 g khí ở đktc etilen có thể tích là
A. 28 lít. B. 5,6 lít. C. 11,2 lít. D. 14 lít.
Câu 5. Benzen không phản ứng với
A. Br2/Fe. B. O2. C. H2 D. dung dịch Br2
Câu 6. Cho natri tác dụng với rượu etylic, chất tạo thành là
A. H2, CH3CH2ONa. B. H2, NaOH.
C. NaOH, H2O. D. CH3CH2ONa, NaOH.
Câu 7. Chất dùng điều chế etylaxetat là
A. axit axe, natri hiđroxit, nước.
B. axit axe, rượu etylic, axit clohiđric.
C. rượu etylic, nước và axit sunfuric đặc.
D. rượu etylic, axit axe và axit sunfuric đặc.
Câu 8. Đốt cháy 46 g chất hữu cơ A thu được 88 g CO2 và 54 g H2O. Trong A có các nguyên tố
A. C. B. C, H. C. C, H, O D. C, O
II. Tự luận (6 điểm)
Câu 9. (1,5 điểm) Viết phương trình hoá học thực hiện dãy chuyển hoá sau:

Câu 10. (2 điểm) Trình bày phương pháp hoá học để nhận biết 3 chất lỏng: benzen, rượu etylic và axit axe ? Viết phương trình hoá học.
Câu 11.(2,5 điểm) Cho 4 lít hỗn hợp etilen và metan ở đktc vào dung dịch brôm, dung dịch brom nhạt màu dần. Sau phản ứng người ta thu được 18,8 g đi brom etan.
a) Viết phương trình phản ứng xảy ra?
b) Tính khối lượng brôm tham gia phản ứng?
c) Xác định thành phần phần trăm về thể tích của mỗi khí trong hỗn hợp?
(C = 12 ; H = 1 ; Br = 80)

câu 9: k=-3
vì có 1 đẳng thức này nè: \(x^3+y^3+z^3-3xyz=\left(x+y+z\right)\left(x^2+y^2+z^2-xy-yz-zx\right)\)
câu 10 thì tui ko bt
Câu 10: Vì đây là violympic nên mk sẽ làm khá tắt!
Đặt \(f\left(x\right)=ax^3+bx^2+c\)
Áp dụng định lí Be-du ta có: f(a) = r
\(\left\{{}\begin{matrix}f\left(-2\right)=-8a+4b+c=0\\f\left(1\right)=a+b+c=6\\f\left(-1\right)=-a+b+c=4\end{matrix}\right.\)
Bấm máy tính để giải hệ PT => \(\left\{{}\begin{matrix}a=1\\b=1\\c=4\end{matrix}\right.\)
Vậy ......................

1:
1: \(2\sqrt{12}+3\sqrt{18}-3\sqrt{75}-\sqrt{50}\)
\(=4\sqrt{3}-15\sqrt{3}+9\sqrt{2}-5\sqrt{2}\)
\(=-11\sqrt{3}+4\sqrt{2}\)
2: \(\sqrt{16-6\sqrt{7}}+\sqrt{\left(3+\sqrt{7}\right)^2}\)
\(=\sqrt{\left(3-\sqrt{7}\right)^2}+\sqrt{\left(3+\sqrt{7}\right)^2}\)
\(=\left|3-\sqrt{7}\right|+\left|3+\sqrt{7}\right|\)
\(=3-\sqrt{7}+3+\sqrt{7}=6\)
3:
\(\dfrac{6}{\sqrt{7}-1}+\dfrac{4}{\sqrt{7}-3}+\dfrac{7}{\sqrt{7}}\)
\(=\dfrac{6\left(\sqrt{7}+1\right)}{7-1}-\dfrac{4}{3-\sqrt{7}}+\sqrt{7}\)
\(=\sqrt{7}+1+\sqrt{7}-\dfrac{4\left(3+\sqrt{7}\right)}{2}\)
\(=2\sqrt{7}+1-2\left(3+\sqrt{7}\right)\)
=1-6
=-5
2:
a: ĐKXĐ: x>=5
\(5\sqrt{x-5}+\sqrt{4x-20}-\sqrt{9x-45}=12\)
=>\(5\sqrt{x-5}+2\sqrt{x-5}-3\sqrt{x-5}=12\)
=>\(4\sqrt{x-5}=12\)
=>\(\sqrt{x-5}=3\)
=>x-5=9
=>x=14(nhận)
2:
ĐKXĐ: \(x\in R\)
\(\sqrt{4x^2-20x+25}=1\)
=>\(4x^2-20x+25=1\)
=>(2x-5)2=1
=>\(\left[{}\begin{matrix}2x-5=1\\2x-5=-1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}2x=6\\2x=4\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=3\\x=2\end{matrix}\right.\)


b) Thay x=0 và y=0 vào (d), ta được:
\(2m\cdot0+3-m-0=0\)
\(\Leftrightarrow3-m=0\)
hay m=3
c) Thay x=2 và y=0 vào (d), ta được:
\(2m\cdot2+3-m-2=0\)
\(\Leftrightarrow3m=-1\)
hay \(m=-\dfrac{1}{3}\)

\(=\left(\dfrac{\sqrt{5}\left(\sqrt{3}-2\right)}{\sqrt{3}-2}+\dfrac{\sqrt{6}\left(\sqrt{3}+\sqrt{2}\right)}{\sqrt{3}+\sqrt{2}}-\dfrac{\sqrt{6}-\sqrt{5}}{\left(\sqrt{6}-\sqrt{5}\right)\left(\sqrt{6}+\sqrt{5}\right)}\right):\sqrt{\dfrac{5}{2}}\)
\(=\left(\sqrt{5}+\sqrt{6}-\sqrt{6}+\sqrt{5}\right):\dfrac{\sqrt{5}}{\sqrt{2}}\)
\(=2\sqrt{5}.\dfrac{\sqrt{2}}{\sqrt{5}}=2\sqrt{2}\)
a) Ta có: \(\left(\dfrac{\sqrt{15}-\sqrt{20}}{\sqrt{3}-2}+\dfrac{3\sqrt{2}+2\sqrt{3}}{\sqrt{3}+\sqrt{2}}-\dfrac{1}{\sqrt{6}+\sqrt{5}}\right):\sqrt{\dfrac{5}{2}}\)
\(=\left(\sqrt{5}+\sqrt{6}-\sqrt{6}+\sqrt{5}\right):\dfrac{\sqrt{10}}{2}\)
\(=2\sqrt{5}\cdot\dfrac{2}{\sqrt{10}}=2\sqrt{2}\)


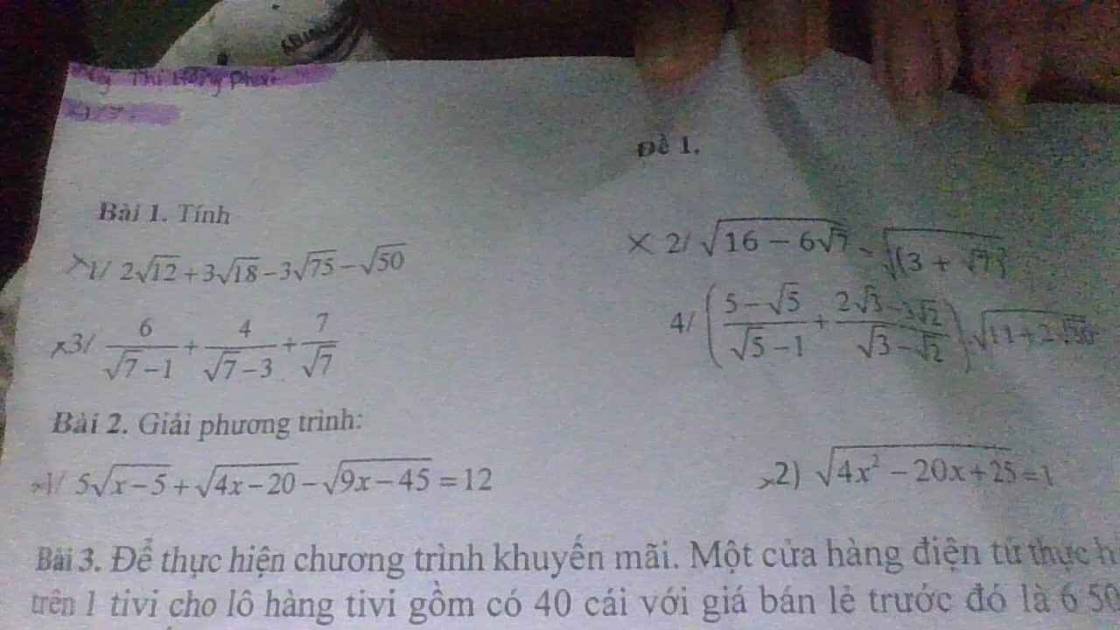

 Giải giúp tớ với ạ, tớ cần gấp lắm
Giải giúp tớ với ạ, tớ cần gấp lắm