
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Câu 6: Để hàm số y=(1-m)x+3 nghịch biến trên R thì 1-m<0
=>m>1
=>Chọn B
Câu 7: D
Câu 10: (D)//(D')
=>\(\left\{{}\begin{matrix}3m+1=2\left(m+1\right)\\-2\ne-2\left(loại\right)\end{matrix}\right.\Leftrightarrow m\in\varnothing\)
=>Chọn D
Câu 11: \(x^2+2x+2=\left(x+1\right)^2+1>=1>0\forall x\)
=>\(\sqrt{x^2+2x+2}\) luôn xác định với mọi số thực x
=>Chọn A
Câu 12: Để hai đường thẳng y=x+3m+2 và y=3x+2m+3 cắt nhau tại một điểm trên trục tung thì \(\left\{{}\begin{matrix}1\ne3\left(đúng\right)\\3m+2=2m+3\end{matrix}\right.\)
=>3m+2=2m+3
=>m=1
=>Chọn C

1:
a: =12/10-7/10=5/10=1/2
b: \(=\dfrac{4}{13}-\dfrac{4}{13}+\dfrac{-5}{11}-\dfrac{6}{11}=-\dfrac{11}{11}=-1\)
2:
a: x+2/7=-11/7
=>x=-11/7-2/7=-13/7
b: (x+3)/4=-7/2
=>x+3=-14
=>x=-17

6.B
Hàm nghịch biến trên R khi:
\(1-m< 0\Rightarrow m>1\)
5.B
Đồ thị đi qua A nên:
\(-1=2a-2\Rightarrow2a=1\Rightarrow a=\dfrac{1}{2}\)

\(M\left(2;6\right)\in y=ax+5\Leftrightarrow6=a\cdot2+5\Rightarrow a=\dfrac{1}{2}\)

10D.
Hai đường thẳng (D) và (D') cùng đi qua điểm (0;-2) nên chúng không bao giờ song song nhau
11.A
\(x^2+2x+2=\left(x+1\right)^2+1>0;\forall x\in R\)
12.C
Hai đồ thị cắt nhau tại 1 điểm trên trục tung khi:
\(3m+2=3+2m\Rightarrow m=1\)
10D.
Hai đường thẳng (D) và (D') cùng đi qua điểm (0;-2) nên chúng không bao giờ song song nhau
11.A
x2+2x+2=(x+1)2+1>0;∀x∈Rx2+2x+2=(x+1)2+1>0;∀x∈R
12.C
Hai đồ thị cắt nhau tại 1 điểm trên trục tung khi:
3m+2=3+2m⇒m=1

Câu 2:
\(3x^2-3x-1=0(*)\)
Theo định lí Vi-ét ta có
\(\begin{cases} S=x_1+x_2=\frac{3}{3}=1\\ P=x_1.x_2=\frac{-1}{3} \end{cases} \)
Theo định lí Vi-ét đảo ta lại có:
Hai nghiệm \(x_1;x_2\) là nghiệm của phương trình: \(X^2-SX+P=0(1)\)
\(\Leftrightarrow X^2-X-\frac{1}{3}=0\)
Ta có: \(\Delta=1+\frac{1}{3}=\frac{4}{3} > 0\)
Vậy phương trình (1) có hai nghiệm phân biệt:
\(\begin{cases} X_1=\frac{3+\sqrt{\frac{4}{3}}}{6}\\ X_2=\frac{3-\sqrt{\frac{4}{3}}}{6} \end{cases} \)
\(\Leftrightarrow \begin{cases} X_1=\frac{3+\sqrt{21}}{6}\\ X_2=\frac{3-\sqrt{21}}{6} \end{cases} \)
Do đó phương trình (*) có hai nghiệm:
\(\left[\begin{array}{} \begin{cases} X_1=\frac{3+\sqrt{21}}{6}\\ X_2=\frac{3-\sqrt{21}}{6} \end{cases}\\ \begin{cases} X_1=\frac{3-\sqrt{21}}{6}\\ X_2=\frac{3+\sqrt{21}}{6} \end{cases} \end{array} \right.\)
\(\Rightarrow \left | x_1-x_2 \right |=\left | x_2-x_1 \right |\)
\(\Rightarrow \left | x_1-x_2 \right |=\left | \frac{3-\sqrt{21}-3-\sqrt{21}}{6} \right |=\left | \frac{-\sqrt{21}}{3} \right |=\frac{\sqrt{21}}{3}\)
Câu 3: \(\begin{cases} x+3y=7\sqrt{2}\\ -2x+y=0 \end{cases} \)
\(\Leftrightarrow \begin{cases} 7x=7\sqrt{2}(1)\\ y=2x \end{cases} \)
Xét phương trình (1) ta có:
\(x=\sqrt{2}\)
\(\Rightarrow y=2\sqrt{2}\)
Vậy hệ phương trình có nghiệm\((x,y)=(\sqrt{2},2\sqrt{2})\)
Câu 4:
Gọi chiều rộng của thửa ruộng là y(m)
Gọi chiều dài của thửa ruộng là x(m)
Điều kiện: x,y>0
Vì diện tích của thửa ruộng hình chữ nhật là \(10000m^2\) nên ta có phương trình:
\(x.y=10000(1) \)
Vì khi tăng chiều rộng của thửa ruộng thêm 20 m và giảm chiều dài đi 50 m thì diện tích thửa ruộng tăng thêm \(500m^2\) nên ta phương trình:
\((y+20).(x-50)=10000+500(2)\)
Từ phương trình (1) và (2) ta có hệ phương trình:
\(\begin{cases} x.y=10000\\ (y+20).(x-50)=10500 \end{cases} \)
Muộn rồi nên bạn tự giải phương trình này được nha:(
Giải phương trình trên ta nhận được nghiệm(x,y)=(200,50)
Do đó chiều rộng của thửa ruộng là 50m
chiều dài của thửa ruộng là 200m

DKXD: \(x\ge2\)
\(\Leftrightarrow\dfrac{2}{5}.5\sqrt{x-2}=6\\ \Leftrightarrow\sqrt{x-2}=6\\ \Leftrightarrow x-2=36\\ \Leftrightarrow x=38\)
\(\dfrac{2}{5}\sqrt{25x-50}=6\)
⇔ \(\sqrt{25x-50}=15\)
⇔ \(25x-50=225\)
⇔ \(25x=275\)
⇔ \(x=11\)

Kẻ OM vuông óc với CD
Vì CD là 1 dây của (O)
=> M là trung điểm của CD
=> MC = MD
Có: AH // BK (cùng vuông góc với CD)
=> AHKB là Hình thang
Lại có: OM vuông góc với CD; O là trung điểm của AB
=> M là trung điểm của HK
=> MH = MK
Có: \(\left\{{}\begin{matrix}HD+MD=HM\\MC+CK=MK\end{matrix}\right.\)
Mà: MH = MK (cmt) và MD = MC (cmt)
=> HD = CK
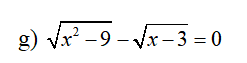


 Mọi người giúp mình với, giải chi tiết (+giải thích giúp mình nha), cảm ơn mọi người rất nhiều lun =)
Mọi người giúp mình với, giải chi tiết (+giải thích giúp mình nha), cảm ơn mọi người rất nhiều lun =)
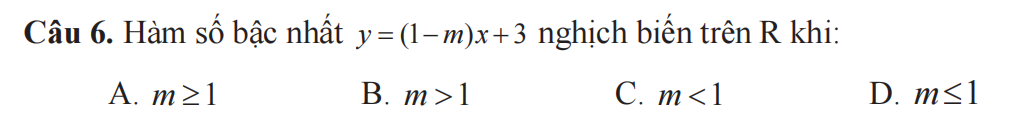
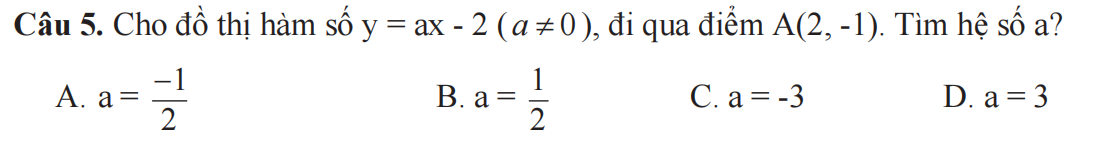



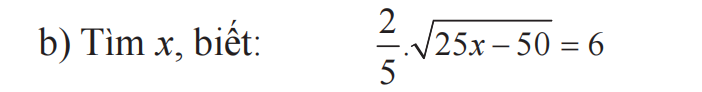
ĐKXĐ: \(x\ge3\)
\(\sqrt{\left(x-3\right)\left(x+3\right)}-\sqrt{x-3}=0\)
\(\Leftrightarrow\sqrt{x-3}\left(\sqrt{x+3}-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}\sqrt{x-3}=0\\\sqrt{x+3}=1\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x-3=0\\x+3=1\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=3\\x=-2\left(ktm\right)\end{matrix}\right.\)