giải giúp mình nha
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
Giúp mình với aa (Giải chi tiết + nếu được thì thêm lời giải thích ở cuối bài làm giúp mình nha 
)
HQ
Hà Quang Minh
Giáo viên
25 tháng 9 2023
\(2\left(x-3\right)^4-3^2=503\\ \Rightarrow2\left(x-3\right)^4=512\\ \Rightarrow\left(x-3\right)^4=256\\ \Rightarrow\left[{}\begin{matrix}x-3=4\\x-3=-4\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=7\\x=-1\end{matrix}\right.\)
CK
1
7 tháng 5 2022
\(f(x)=ax^2+bx+6\)
Để \(f(x)\) là đa thức bậc \(1\) thì \(ax^2=0\)
\(→a=0\)
Thay \(x=1\) vào \(f(x)=ax^2+bx+6\)
\(f(1)=b.1+6=b+6\)
Mà \(f(1)=3\)
\(\Rightarrow b+6=3\Rightarrow b=3−6\Rightarrow b=−3\)
Vậy \(a=0;b=−3\)
3T
1
18 tháng 6 2023
4:
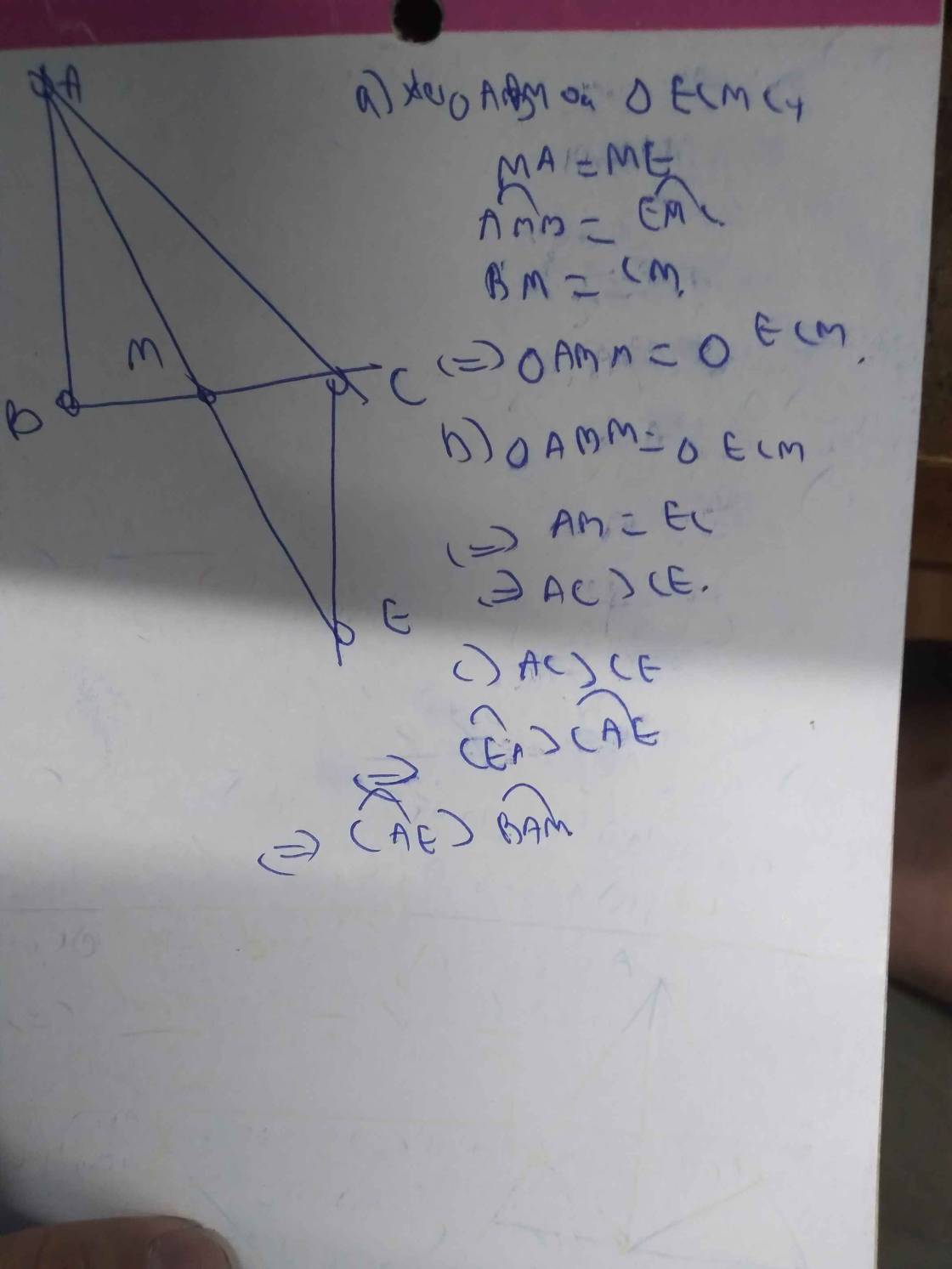
a: Xét tứ giác ABDC có
M là trung điểm chung của AD và BC
góc BAC=90 độ
=>ABDC là hcn
=>ΔACD vuông tại C
b: Xét ΔKAB vuông tại A và ΔKCD vuông tại C có
KA=KC
AB=CD
=>ΔKAB=ΔKCD
=>KB=KD
c: Xét ΔACD có
DK,CM là trung tuyến
DK cắt CM tại I
=>I là trọng tâm
=>KI=1/3KD
Xét ΔCAB có
AM,BK là trung tuyến
AM cắt BK tại N
=>N là trọng tâm
=>KN=1/3KB=KI
giải giúp mình nha :<
Giải giúp mình nha!
6 tháng 2 2022
-Hình vẽ:
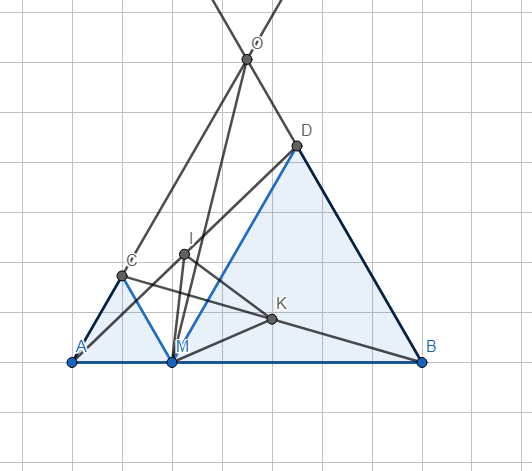
a) -Ta có: \(\widehat{CAM}=60^0\) (△ACM đều), \(\widehat{MBD}=60^0\) (△BDM đều).
=>\(\widehat{CAM}=\widehat{MBD}=60^0\) hay \(\widehat{OAB}=\widehat{OBA}=60^0\)
=>△ABO đều.
b) -Ta có: \(\widehat{AMC}=60^0\) (△ACM đều) ; \(\widehat{MBD}=60^0\) (△BDM đều).
=.\(\widehat{AMC}=\widehat{MBD}\) mà 2 góc này ở vị trí đồng vị.
=>MC//BO.
-Ta có: \(\widehat{CAM}=60^0\) (△ACM đều) ; \(\widehat{BMD}=60^0\) (△BDM đều).
=.\(\widehat{CAM}=\widehat{BMD}\) mà 2 góc này ở vị trí đồng vị.
=>AC//MD.
-Xét △OCM và △MDO có:
\(\widehat{OMC}=\widehat{MOD}\) (MC//OD và so le trong).
\(OM\) là cạnh chung.
\(\widehat{COM}=\widehat{DMO}\) (OC//MD và so le trong).
=>△OCM = △MDO (c-g-c).
=>\(MC=OD\) (2 cạnh tương ứng) ; \(MD=OC\) (2 cạnh tương ứng).
c) -Ta có: \(\widehat{BMD}+\widehat{AMD}=180^0\) (kề bù).
Mà \(\widehat{BMD}=60^0\) (△BDM đều).
=>\(60^0+\widehat{AMD}=180^0\)
=>\(\widehat{AMD}=120^0\)
-Ta có: \(\widehat{AMC}+\widehat{CMB}=180^0\) (kề bù).
Mà \(\widehat{AMC}=60^0\) (△ACM đều).
=>\(60^0+\widehat{CMB}=180^0\)
=>\(\widehat{CMB}=120^0\)
-Xét △AMD và △CMB có:
\(AM=CM\) (△ACM đều).
\(\widehat{AMD}=\widehat{CMB}=120^0\)
\(MD=MB\) (△BDM đều).
=>△AMD = △CMB (c-g-c).
=>\(AD=BC\) (2 cạnh tương ứng).
d) -Ta có: \(AD=2AI\) (I là trung điểm AD) ; \(BC=2CK\) (K là trung điểm BC).
Mà \(AD=BC\) (cmt) nên \(AI=CK\).
-Xét △AMI và △CMK có:
\(AI=CK\)(cmt).
\(\widehat{MAI}=\widehat{MCK}\)(△AMD = △CMB)
\(AM=CM\) (△ACM đều).
=>△AMI=△CMK (c-g-c).
=>\(MI=MK\) (2 cạnh tương ứng) nên △MIK cân tại M (1).
\(\widehat{AMI}=\widehat{CMK}\)(2 góc tương ứng).
Mà \(\widehat{AMI}=\widehat{AMC}+\widehat{CMI}\) ; \(\widehat{CMK}=\widehat{CMI}+\widehat{IMK}\)
=>\(\widehat{AMC}=\widehat{CMI}\).
Mà \(\widehat{AMC}=60^0\) (△AMC đều).
=>\(\widehat{CMI}=60^0\) (2).
-Từ (1) và (2) suy ra: △MIK đều.
B
2
27 tháng 1 2022
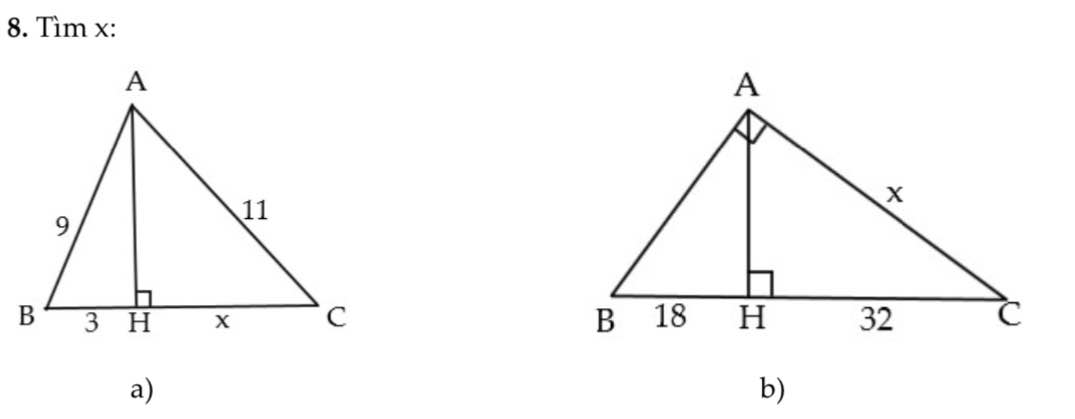
a, Theo định lí Pytago tam giác ABH vuông tại H
\(AH=\sqrt{AB^2-BH}=\sqrt{81-9}=6\sqrt{2}\)
Theo định lí Pytago tam giác AHC vuông tại H
\(HC=x=\sqrt{AC^2-AH^2}=7\)
b, Xét tam giác ABC vuông tại A, đường cao AH
* Áp dụng hệ thức : \(AC^2=HC.BC=1600\Rightarrow AC=x=40\)
VH
2
S
20 tháng 12 2016
x^2 - 3x - 4=0
x^2 - 3x =0+4
x^2 -3x=4
x.x-3x=4
x.(x-3)=4
Suy ra x>3 và x ko thể bằng 3
Vậy x xhir có thể là 4
20 tháng 12 2016
=x^2+x-4x-4
=(x^2+x)-(4x+4)
=x(x+1)-4(x+1)
=(x+1)(x-4)
=>
x=-1
và
x=4
