Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\dfrac{4x+2}{4x-2}+\dfrac{3-6x}{6x-6}\left(dkxd:x\ne\dfrac{1}{2};x\ne1\right)\)
\(=\dfrac{2\left(2x+1\right)}{2\left(2x-1\right)}+\dfrac{3\left(1-2x\right)}{6\left(x-1\right)}\)
\(=\dfrac{2x+1}{2x-1}+\dfrac{1-2x}{2\left(x-1\right)}\)
\(=\dfrac{2x+1}{2x-1}+\dfrac{1-2x}{2x-2}\)
\(=\dfrac{\left(2x+1\right)\left(2x-2\right)}{\left(2x-1\right)\left(2x-2\right)}+\dfrac{\left(1-2x\right)\left(2x-1\right)}{\left(2x-1\right)\left(2x-2\right)}\)
\(=\dfrac{4x^2-2x-2}{\left(2x-1\right)\left(2x-2\right)}+\dfrac{-4x^2+4x-1}{\left(2x-1\right)\left(2x-2\right)}\)
\(=\dfrac{4x^2-2x-2-4x^2+4x-1}{\left(2x-1\right)\left(2x-2\right)}\)
\(=\dfrac{2x-3}{\left(2x-1\right)\left(2x-2\right)}\)
\(=\dfrac{2x-3}{4x^2-6x+2}\)

Lương Tịch bn tham khảo nha
I > Phương pháp dự đoán và quy nạp :
Trong một số trường hợp khi gặp bài toán tính tổng hữu hạn
Sn = a1 + a2 + .... an (1)
Bằng cách nào đó ta biết được kết quả (dự đoán , hoặc bài toán chứng minh khi đã cho biết kết quả). Thì ta nên sử dụng phương pháp này và hầu như thế nào cũng chứng minh được .
Ví dụ 1 : Tính tổng Sn =1+3+5 +... + (2n -1 )
Thử trực tiếp ta thấy : S1 = 1
S2 = 1 + 3 =22
S3 = 1+ 3+ 5 = 9 = 32
... ... ...
Ta dự đoán Sn = n2
Với n = 1;2;3 ta thấy kết quả đúng
giả sử với n= k ( k 1) ta có Sk = k 2 (2)
ta cần phải chứng minh Sk + 1 = ( k +1 ) 2 ( 3)
Thật vậy cộng 2 vế của ( 2) với 2k +1 ta có
1+3+5 +... + (2k – 1) + ( 2k +1) = k2 + (2k +1)
vì k2 + ( 2k +1) = ( k +1) 2 nên ta có (3) tức là Sk+1 = ( k +1) 2
theo nguyên lý quy nạp bài toán được chứng minh
vậy Sn = 1+3=5 + ... + ( 2n -1) = n2
Tương tự ta có thể chứng minh các kết quả sau đây bằng phương pháp quy nạp toán học .
1, 1 + 2+3 + .... + n =
2, 12 + 2 2 + ..... + n 2 =
3, 13+23 + ..... + n3 =
4, 15 + 25 + .... + n5 = .n2 (n + 1) 2 ( 2n2 + 2n – 1 )

sgk toán 8 tập 1
Bài 74. Hai đường chéo của một hình thoi bằng 8cm8cm và 10cm10cm. Cạnh của hình thoi bằng giá trị nào trong các giá trị sau:
(A) 6cm6cm; (B) √41cm41cm
(C) √164cm164cm (D) 9cm9cm ?
Bài giải:
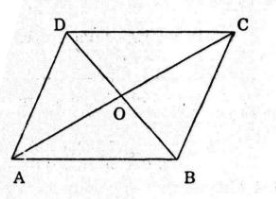
Xét bài toán tổng quát:
ABCDABCD là hình thoi, OO là giao điểm hai đường chéo.
Theo tính của hình thoi hai đường chéo của hình thoi vuông góc và cắt nhau tại trung điểm mỗi đường.
Áp dụng định lí Pytago vào tam giác vuông ABOABO ta có:
AB2=OA2+OB2=(12AC)2+(12BD)2⇒AB=√(12AC)2+(12BD)2=√42+52=√41cmAB2=OA2+OB2=(12AC)2+(12BD)2⇒AB=(12AC)2+(12BD)2=42+52=41cm
Vậy (B) đúng.
Bài 79.
a) Một hình vuông có cạnh bằng 3cm3cm. Đường chéo của hình vuông đó bằng 6cm6cm, √18cm18cm, 5cm5cm hay 4cm4cm ?
b) Đường chéo của một hình vuông bằng 2dm2dm. Cạnh cảu hình vuông đó bằng: 1dm1dm,
32dm32dm, √2dm2dm hay 43dm43dm ?
Bài giải:
a) Gọi đường chéo của hình vuông có độ dài là aa.
Ta có: a2=32+32=18a2=32+32=18
Suy ra a=√18a=18
Vậy đường chéo của hình vuông đó bằng √18cm18cm.
b) Gọi cạnh của hình vuông là aa.
Ta có a2+a2=22⇒2a2=4⇒a2=2⇒a=√2a2+a2=22⇒2a2=4⇒a2=2⇒a=2
Vậy cạnh của hình vuông đó bằng √2dm2dm.

a: ĐKXĐ: \(x\notin\left\{10;-10;\sqrt{10};-\sqrt{10}\right\}\)
b: \(A=\dfrac{5x^3+50x+2x^2+20+5x^3-50x-2x^2+20}{\left(x^2-10\right)\left(x^2+10\right)}\cdot\dfrac{x^2-100}{x^2+4}\)
\(=\dfrac{10x^3+40}{\left(x^2-10\right)\left(x^2+10\right)}\cdot\dfrac{x^2-100}{x^2+4}\)

Lời giải:
a.
Tại $x=5$ thì $B=\frac{5+3}{5-2}=\frac{8}{3}$
b.
\(A=\frac{x^2-x+1}{(x-2)(x+2)}+\frac{2(x+2)}{(x-2)(x+2)}-\frac{x-2}{(x-2)(x+2)}=\frac{x^2-x+1+2(x+2)-(x-2)}{(x-2)(x+2)}\)
\(=\frac{x^2+7}{(x-2)(x+2)}\)
c.
\(P=A:B(x+2)=\frac{x^2+7}{(x-2)(x+2)}:\frac{x+3}{x-2}.(x+2)=\frac{x^2+7}{x+3}\)
Áp dụng BĐT Cô-si:
$x^2+1\geq 2|x|\geq 2x$
$\Rightarrow x^2+7\geq 2x+6=2(x+3)$
$\Rightarrow P\geq \frac{2(x+3)}{x+3}=2$
Vậy $P_{\min}=2$. Giá trị này đạt tại $x^2=1\Leftrightarrow x=\pm 1$ (tm)

\(6-\sqrt{17}=\sqrt{36}-\sqrt{17}\)
Với :
\(\sqrt{36}-\sqrt{17}>\sqrt{31}-\sqrt{17}\)
Mặt khác :
\(\sqrt{31}-\sqrt{17}>\sqrt{31}-\sqrt{19}\)
Nên :
\(6-\sqrt{17}>\sqrt{31}-\sqrt{19}\)
Cách khác:
Ta có: \(\left(\sqrt{31}-\sqrt{19}\right)^2=50-2\sqrt{589}\)
\(\left(6-\sqrt{17}\right)^2=53-12\sqrt{17}=50+3-12\sqrt{17}\)
mà \(-2\sqrt{589}< 3-12\sqrt{17}\)
nên \(\sqrt{31}-\sqrt{19}>6-\sqrt{17}\)
 Các bạn giải giúp mình với ạ, phần a ghi chi tiết bước giải hộ mình nhé. Mình cám ơn ạ! (Mai mình nộp rồi nên nhanh giúp mình ạ T.T)
Các bạn giải giúp mình với ạ, phần a ghi chi tiết bước giải hộ mình nhé. Mình cám ơn ạ! (Mai mình nộp rồi nên nhanh giúp mình ạ T.T)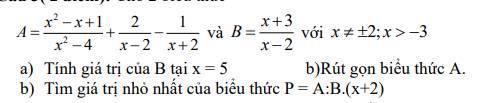
\(1023456^3=1023456.1023456.1023456=\)kết quả lớn lắm
vay co cach nao tinh dc k