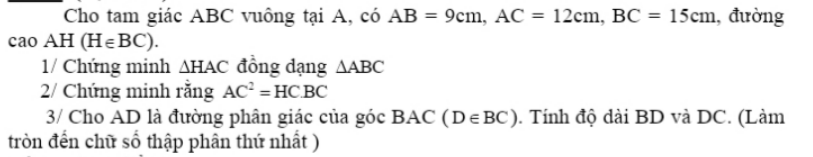K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NL
2
NV
Nguyễn Việt Lâm
Giáo viên
6 tháng 1 2022
\(3x\left(x-y\right)+x-y\)
\(=3x\left(x-y\right)+1\left(x-y\right)\)
\(=\left(x-y\right)\left(3x+1\right)\)
17 tháng 4 2022
\(\left|2x-3\right|=3-2x\)
\(ĐK:x\le\dfrac{3}{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-3=3-2x\\3-2x=3-2x\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{3}{2}\\0=0\left(đúng\right)\end{matrix}\right.\)
Vậy \(S=\left\{x\in R;x=\dfrac{3}{2}\right\}\)
21 tháng 4 2022
1/ Xét \(\Delta ABC\) và \(\Delta HAC\) có:
∠A = ∠AHC = 90 độ
∠C là góc chung
Do đó: △ABC ∼ △HAC (g . g)
2/ Ta có: \(\Delta HAC\sim\Delta ABC\)
\(\Rightarrow\dfrac{AC}{HC}=\dfrac{BC}{AC}\)
\(\Rightarrow AC.AC=HC.BC\)
\(\Rightarrow AC^2=HC.BC\) (đpcm)
3/ Đặt BD là x, theo tính chất đường phân giác, ta có:
\(\dfrac{AB}{AC}=\dfrac{BD}{DC}\Rightarrow\dfrac{9}{12}=\dfrac{x}{15-x}\)
\(\Rightarrow9\left(15-x\right)=12x\)
\(\Rightarrow135-9x=12x\)
\(\Rightarrow135=12x+9x\)
\(\Rightarrow135=21x\)
\(\Rightarrow x\approx6,4\)
Độ dài của DC là: \(15-x\Rightarrow15-6,4=8,6\)
Vậy BD = 6,4 cm và DC = 8,6 cm
MN
6
30 tháng 7 2021
Bài cuối mình không thấy rõ đề nhưng mình đoán là thế này bạn nhé.
PL
2
30 tháng 8 2021
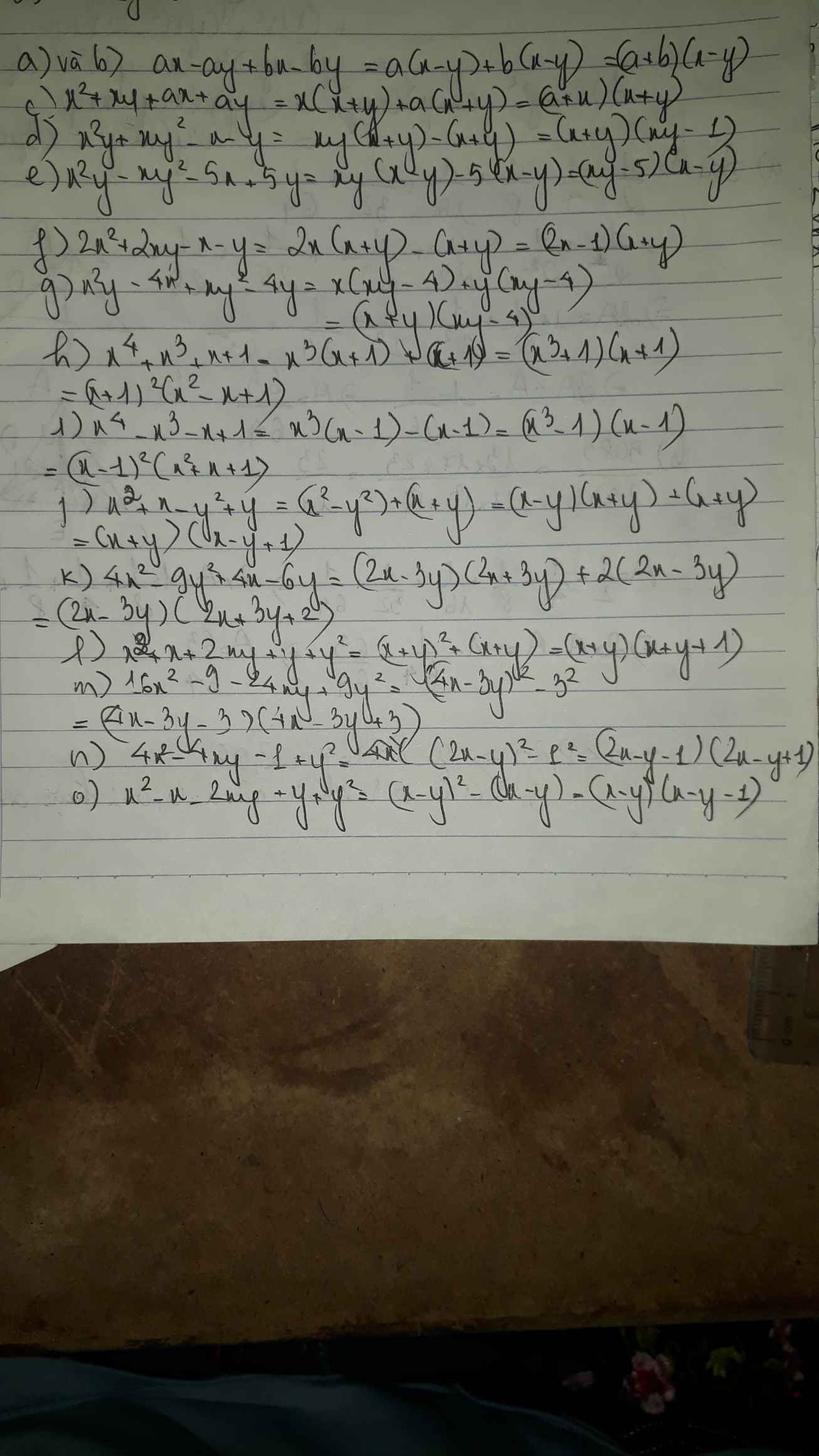
Câu 3:
a: Ta có: \(2x\left(3x-1\right)-\left(x-3\right)\left(6x+2\right)\)
\(=6x^2-2x-6x^2-2x+18x+6\)
=14x+6
b: Ta có: \(2x\left(x+7\right)-3x\left(x+1\right)\)
\(=2x^2+14x-3x^2-3x\)
\(=-x^2+11x\)
30 tháng 8 2021
Câu 2:
a: Ta có: \(\left(-8x^5+12x^3-16x^2\right):4x^2\)
\(=-8x^5:4x^2+12x^3:4x^2-16x^2:4x^2\)
\(=-2x^3+3x-4\)
b: Ta có: \(\left(12x^3y^3-18x^2y+9xy^2\right):6xy\)
\(=12x^3y^3:6xy-18x^2y:6xy+9xy^2:6xy\)
\(=2x^2y^2-3x+\dfrac{3}{2}y\)
c: Ta có: \(\dfrac{x^3-11x^2+27x-9}{x-3}\)
\(=\dfrac{x^3-3x^2-8x^2+24x+3x-9}{x-3}\)
\(=x^2-8x+3\)
d: Ta có: \(\dfrac{6x^4-13x^3+7x^2-x-5}{3x+1}\)
\(=\dfrac{6x^4+2x^3-15x^3-5x^2+12x^2+4x-5x-\dfrac{5}{3}-\dfrac{10}{3}}{3x+1}\)
\(=2x^3-5x^2+4x-\dfrac{5}{3}-\dfrac{\dfrac{10}{3}}{3x+1}\)
B
8 tháng 9 2021
B6
a)goij 3 stn đó là a,a+1 và a+2
từ đề bài ta có (a+1)(a+2)-a(a+1)=100
=>a^2+3a+2-a^2-a=100
=>2a=98
=>a=49
=>các số tm đề ra:49,50,51
b)đặt 3 số đó là 2k,2k+2,2k+4
ta có (2k+4)(2k+2)-(2k+2)2k=256
=>4k^2+12k+8-4k^2-4k=256
=>8k=248
=>k=31
=>3 số đó là 62,64,66
c)gọi 3 số đó là 2m+1,2m+3,2m+5
ta có (2m+3)(2m+5)-(2m+3)(2m+1)=68
=>4m^2+16m+15-4m^2-8m+3=68
=>10m=50
=>m=5
=>3 số đó là 101,103,105
11 tháng 9 2021
a) x16+1 = (x16+2x8+1) - 2x8 = (x8+1)2-2x8 = \(\left(x^8-\sqrt{2}x^4+1\right)\left(x^8+\sqrt{2}x^4+1\right)\)
b) 81x4+144 = (81x4+216x2+144)-216x2 = (9x2+12)2-216x2
\(=\left(9x^2-6\sqrt{6}x+12\right)\left(9x^2+6\sqrt{6}x+12\right)\)
c) \(4x^4+9=\left(4x^4+12x^2+9\right)-12x^2=\left(2x^2+3\right)^2-12x^2\)
\(=\left(2x^2-2\sqrt{3}x+3\right)\left(2x^2+2\sqrt{3}x+3\right)\)
d) \(16x^4y^4+1=\left(16x^4y^4+4x^2y^2+1\right)-4x^2y^2=\left(4x^2y^2+1\right)^2-4x^2y^2=\left(4x^2y^2-2xy+1\right)\left(4x^2y^2+2xy+1\right)\)
5 tháng 5 2021
Bài 4:
a) Xét ΔHBA vuông tại H và ΔABC vuông tại A có
\(\widehat{ABC}\) chung
Do đó: ΔHBA\(\sim\)ΔABC(g-g)
5 tháng 5 2021
c) Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=12^2+16^2=400\)
hay BC=20(cm)
Vậy: BC=20cm
