
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


BẠN CÓ THỂ TẢI QANDA VỀ MÁY ĐIỆN THOẠI VÀ TRA HAI CÂU NÀY Ở TRÊN ỨNG DỤNG QANDA LÀ CÓ KẾT QUẢ NGAY. NẾU KO CÓ THÌ BẤM VÀO MỤC HỎI GIA SƯ LÀ SẼ CÓ GIA SƯ GIẢI NGAY CHO BẠN.

a: Xét ΔBAD vuông tại A và ΔBED vuông tại E có
BD chung
góc ABD=góc EBD
=>ΔBAD=ΔBED
=>AD=ED
b: Xét ΔBEF vuông tại E và ΔBAC vuông tại A có
BE=BA
góc EBF chung
=>ΔBEF=ΔBAC
=>BF=BC
2BF=BF+BC>FC

a) Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow AC^2=BC^2-AB^2=10^2-6^2=64\)
hay AC=8(cm)
Vậy: AC=8cm
c) Xét tam giác BIC có:
BHI=CAB=90°
=>IH và CB là hai đường cao của tam giác BIC
Mà IH và CB cắt nhau tại E
=> E là trực tâm của tam giác BIC
=>BE vuông góc với IC
Mà BE cũng là đường phân giác của góc B
=> Tam giác BIC cân tại B
=>BE cũng là đường trung trực của đoạn thẳng IC

\(D=10\cdot\left(-2.5\right)\cdot0.4\cdot\left(-0.1\right)\)
\(=10\cdot1\cdot2.5\cdot0.4\)
=10


Ta có: \(\left(x-2\right)^2-\left(x-3\right)\left(x+3\right)+4\left(x-7\right)\)
\(=x^2-4x+4-x^2+3^2+4x-28\\ =\left(x^2-x^2\right)-\left(4x-4x\right)+\left(4+3^2-28\right)\\=-15 \)
⇒ Gía trị của biểu thức \(\left(x-2\right)^2-\left(x-3\right)\left(x+3\right)+4\left(x-7\right)\) không phụ thuộc vào biến \(x\) \(\left(đcpcm\right)\)
3
a,\(\left(x-5\right)\left(x+5\right)-x\left(x-4\right)=0\)
\(\Leftrightarrow x^2-5^2-x^2+4x=0\\ \Leftrightarrow\left(x^2-x^2\right)+4x-5^2\\ \Leftrightarrow4x=25\\ \Leftrightarrow x=\dfrac{25}{4}\)
Vậy....
b,\(\left(2x-1\right)\left(4x^2+2x+1\right)-\left(x-1\right)\left(x+1\right)=0\)
\(\Leftrightarrow8x^3-1-\left(x^2-1^2\right)=0\\ \Leftrightarrow8x^3-x^2-\left(1-1\right)=0\\ \Leftrightarrow8x^3-x^2=0\\ \Leftrightarrow x^2\left(8x-1\right)=0\\ \Rightarrow\left[{}\begin{matrix}x^2=0\\8x-1=0\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=0\\x=\dfrac{1}{8}\end{matrix}\right.\)
Vậy...
c,\(\left(x-3\right)^2+x\left(2x-3\right)=3x^2-6x+9\)
\(\Leftrightarrow x^2-6x+9+2x^2-3x=3x^2-6x+9\\ \Leftrightarrow x^2+2x^2-3x^2-6x+6x-3x=9-9\\ \Leftrightarrow-3x=0\\ \Leftrightarrow x=0\)
Vậy...

a: Xét ΔDOE vuông tại O và ΔKOE vuông tại O có
EO chung
\(\widehat{DEO}=\widehat{KEO}\)
Do đó: ΔDOE=ΔKOE
b: Xét ΔEDI vàΔEKI có
ED=EK
\(\widehat{DEI}=\widehat{KEI}\)
EI chung
Do đó: ΔEDI=ΔEKI
Suy ra: \(\widehat{EDI}=\widehat{EKI}=90^0\)
hay IK\(\perp\)FE
c: Xét ΔDIQ vuông tại D và ΔKIF vuông tại K có
ID=IK
\(\widehat{DIQ}=\widehat{KIF}\)
Do đó: ΔDIQ=ΔKIF
Suy ra: IQ=IF

Câu 3:
a: \(BD=\sqrt{BC^2-DC^2}=4\left(cm\right)\)
b: \(\widehat{A}=180^0-2\cdot70^0=40^0< \widehat{B}\)
nên BC<AC=AB
c: Xét ΔEBC vuông tại E và ΔDCB vuông tại D có
BC chung
\(\widehat{EBC}=\widehat{DCB}\)
Do đó:ΔEBC=ΔDCB
d: Xét ΔOBC có \(\widehat{OBC}=\widehat{OCB}\)
nên ΔOBC cân tại O
Câu 2
a) Thay y = -2 vào biểu thức đã cho ta được:
2.(-2) + 3 = -1
Vậy giá trị của biểu thức đã cho tại y = -2 là -1
b) Thay x = -5 vào biểu thức đã cho ta được:
2.[(-5)² - 5] = 2.(25 - 5) = 2.20 = 40
Vậy giá trị của biểu thức đã cho tại x = -5 là 40

ta có: x/2 + 3/y = 5/4
=> 5/4 - x/2 = 3/y
=> 5/4 - 2x/4 = 3/y
=> (5 -2x)/4 = 3/y
=> y(5 - 2x) = 12
Suy ra: y; 5-2x thuộc ước của 12 = 1; -1; 2; -2; 3;-3;4;-4;6;-6;12;-12 (1)
Vì x, y là số nguyên dương nên 2x>0 => 5 - 2x>4
Nên từ (1) suy ra 5-2x = 6;12
Ta có bảng:
| 5-2x | 6 | 12 |
| y | 2 | 1 |
| 2x | -1 | -7 |
| x | không có | không có |
Vậy không có giá trị để x,y thỏa mãn đề bài
Ta có : \(\frac{x}{2}+\frac{3}{y}=\frac{5}{4}\)
\(\Rightarrow\frac{5}{4}-\frac{x}{2}=\frac{3}{y}\)
\(\Rightarrow\frac{5}{4}-\frac{2x}{4}=\frac{3}{y}\)
\(\Rightarrow\frac{5-2x}{4}=\frac{3}{y}\)
\(\Rightarrow y\left(5-2x\right)=12\)
\(\Rightarrow\) y = 5 - 2x \(\in\) Ư(12) = { 1 ; -1 ; 2 ; -2 ; 3 ; -3 ; 4 ; -4 ; 6 ; -6 ; 12 ; -12 }
Vì x ; y là số nguyên dương nên 2x > 0 \(\rightarrow\) 5 - 2x > 4
\(\Rightarrow\) 5 - 2x = 6 ; 12 nên ta có bảng sau :
| 5 - 2x | 6 | 12 |
| y | 2 | 1 |
| 2x | -1 | -7 |
| x | không có | không có |
Vậy không có x ; y để thỏa mãn đề bài .
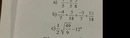


 Giúp dùm mik câu b với ạ!! Vẽ hình câu b giúp mik luôn nhé
Giúp dùm mik câu b với ạ!! Vẽ hình câu b giúp mik luôn nhé




c) \(\frac{1}{2}.\sqrt{\frac{49}{9}}-12^0=\frac{1}{2}.\frac{7}{3}-1=\frac{7}{6}-1=\frac{1}{6}\)