
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Câu 5:
\(\dfrac{13}{6}+x=-2,4\)
\(\Rightarrow\dfrac{13}{6}+x=-\dfrac{12}{5}\)
\(\Rightarrow x=-\dfrac{12}{5}-\dfrac{13}{6}\)
\(\Rightarrow x=-\dfrac{137}{30}\)
Câu 6:
\(3,7-x=\dfrac{7}{10}\)
\(\Rightarrow\dfrac{37}{10}-x=\dfrac{7}{10}\)
\(\Rightarrow x=\dfrac{37}{10}-\dfrac{7}{10}\)
\(\Rightarrow x=3\)
Câu 7:
\(\dfrac{3}{7}+x=\dfrac{2}{14}\)
\(\Rightarrow\dfrac{3}{7}+x=\dfrac{1}{7}\)
\(\Rightarrow x=\dfrac{1}{7}-\dfrac{3}{7}\)
\(\Rightarrow x=-\dfrac{2}{7}\)
Câu 8:
\(\dfrac{3}{7}\cdot y=\dfrac{-2}{5}\)
\(\Rightarrow y=\dfrac{-2}{5}:\dfrac{3}{7}\)
\(\Rightarrow y=\dfrac{-2}{5}\cdot\dfrac{7}{3}\)
\(\Rightarrow y=-\dfrac{14}{15}\)


Bài 1:
a, \(\dfrac{2}{3}\) + \(\dfrac{1}{5}\). \(\dfrac{10}{7}\)
= \(\dfrac{2}{3}\) + \(\dfrac{2}{7}\)
= \(\dfrac{20}{21}\)
b, \(\dfrac{7}{12}\) - \(\dfrac{27}{7}\). \(\dfrac{1}{18}\)
= \(\dfrac{7}{12}\) - \(\dfrac{3}{14}\)
= \(\dfrac{31}{84}\)
c, \(\dfrac{3}{10}\). \(\dfrac{-5}{6}\) - \(\dfrac{1}{8}\)
= - \(\dfrac{1}{4}\) - \(\dfrac{1}{8}\)
= - \(\dfrac{3}{8}\)
d, - \(\dfrac{4}{9}\): \(\dfrac{8}{3}\) + \(\dfrac{1}{18}\)
= - \(\dfrac{1}{6}\) + \(\dfrac{1}{18}\)
= - \(\dfrac{1}{9}\)
e, {[(\(\dfrac{1}{2}\) - \(\dfrac{2}{3}\))2 : 2 ] - 1}. \(\dfrac{4}{5}\)
= {[ (-\(\dfrac{1}{6}\))2 : 2] - 1}. \(\dfrac{4}{5}\)
= { [\(\dfrac{1}{36}\) : 2] - 1}. \(\dfrac{4}{5}\)
= { \(\dfrac{1}{72}\) - 1}. \(\dfrac{4}{5}\)
=- \(\dfrac{71}{72}\).\(\dfrac{4}{5}\)
= -\(\dfrac{71}{90}\)


Bài 16
a) \(A=\dfrac{n+1}{n+2}\)
Gọi ƯCLN(n+1;n+2) là x ( \(x\in N\) *)
\(\Rightarrow\) \(\left\{{}\begin{matrix}\left(n+1\right)⋮x\\\left(n+2\right)⋮x\end{matrix}\right.\)
\(\Rightarrow\) \(\left(n+2\right)-\left(n+1\right)\) \(⋮x\)
\(\Rightarrow\) \(1\) \(⋮x\)
\(\Rightarrow\) x = 1 \(\Rightarrow\) ƯCLN(n+1;n+2)=1
Vậy A là phân số tối giản ( vì có ƯCLN = 1)
b) \(B=\dfrac{n+1}{3n+4}\)
Gọi ƯCLN(n+1;3n+4) là d ( \(d\in N\) *)
\(\Rightarrow\) \(\left\{{}\begin{matrix}n+1⋮d\\3n+4⋮d\end{matrix}\right.\)
\(\Rightarrow\) \(\left\{{}\begin{matrix}3n+3⋮d\\3n+4⋮d\end{matrix}\right.\)
\(\Rightarrow\) (3n+4)-(3n+3) chia hết cho d
\(\Rightarrow\) \(1⋮d\)
\(\Rightarrow\) d =1
Vậy B là phân số tối giản.
Mấy phần kia tương tự
c: Gọi d=ƯCLN(3n+2;5n+3)
=>3n+2 chia hết cho d và 5n+3 chia hết cho d
=>15n+10 chia hết cho d và 15n+9 chia hết cho d
=>1 chia hết cho d
=>ƯCLN(3n+2;5n+3)=1
=>PSTG
d: Gọi d=ƯCLN(12n+1;30n+2)
=>12n+1 và 30n+2 đều chia hết cho d
=>60n+5 chia hết cho d và 60n+4 chia hết cho d
=>1 chia hết cho d
=>d=1
=>PSTG

\(c,-\dfrac{8}{13}+\left(-\dfrac{7}{5}-x\right)=-\dfrac{1}{2}\\ -\dfrac{7}{5}-x=-\dfrac{1}{2}-\dfrac{8}{13}\\ -\dfrac{7}{5}-x=-\dfrac{29}{26}\\ x=-\dfrac{7}{5}-\left(-\dfrac{29}{26}\right)=-\dfrac{37}{130}\\ d,-1\dfrac{1}{7}-\left[-\dfrac{5}{3}+\left(x-\dfrac{7}{3}\right)\right]=-\dfrac{4}{21}\\ -\dfrac{8}{7}-\left[-\dfrac{5}{3}+\left(x-\dfrac{7}{3}\right)\right]=-\dfrac{4}{21}\\ -\dfrac{5}{3}+\left(x-\dfrac{7}{3}\right)=-\dfrac{8}{7}-\left(-\dfrac{4}{21}\right)\\ -\dfrac{5}{3}+\left(x-\dfrac{7}{3}\right)=-\dfrac{20}{21}\\ x-\dfrac{7}{3}=-\dfrac{20}{21}-\left(-\dfrac{5}{3}\right)\\ x-\dfrac{7}{3}=\dfrac{5}{7}\\ x=\dfrac{5}{7}+\dfrac{7}{3}=\dfrac{64}{21}\\ e,-\dfrac{2}{3}-x:\dfrac{1}{2}=\dfrac{2}{5}\\ x:\dfrac{1}{2}=-\dfrac{2}{3}-\dfrac{2}{5}\\ x:\dfrac{1}{2}=-\dfrac{16}{15}\\ x=-\dfrac{16}{15}\times\dfrac{1}{2}=-\dfrac{8}{15}\)
c: -8/13+(-7/5-x)=-1/2
=>x+7/5+8/13=1/2
=>x=1/2-7/5-8/13=-197/130
d: \(\Leftrightarrow-\dfrac{8}{7}+\dfrac{5}{3}-\left(x-\dfrac{7}{3}\right)=\dfrac{-4}{21}\)
=>\(x-\dfrac{7}{3}=\dfrac{-8}{7}+\dfrac{5}{3}+\dfrac{4}{21}=\dfrac{-24+35+4}{21}=\dfrac{18}{21}=\dfrac{6}{7}\)
=>x=6/7+7/3=18/21+49/21=67/21
e: =>x:1/2=-2/3-2/5=-16/15
=>x=-16/15*1/2=-8/15
f: =>-8/5*x=-1/3+4/9=1/9
=>x=-1/9:8/5=-1/9*5/8=-5/72
g: =>-4/5x-1/4+x=-13/3
=>1/5x=-13/3+1/4=-52/12+3/12=-49/12
=>x=-49/12*5=-245/12
h: =>12/7:x-1/2=0 hoặc 2/5x-3/2=0
=>12/7:x=1/2 hoặc 2/5x=3/2
=>x=12/7:1/2=24/7 hoặc x=3/2:2/5=3/2*5/2=15/4

6:
\(2^{225}=\left(2^3\right)^{75}=8^{75}\)
\(3^{150}=\left(3^2\right)^{75}=9^{75}\)
mà 8<9
nên \(2^{225}< 3^{150}\)
4: \(\left|5x+3\right|>=0\forall x\)
=>\(-\left|5x+3\right|< =0\forall x\)
=>\(-\left|5x+3\right|+5< =5\forall x\)
Dấu = xảy ra khi 5x+3=0
=>x=-3/5
1:
\(\left(2x+1\right)^4>=0\)
=>\(\left(2x+1\right)^4+2>=2\)
=>\(M=\dfrac{3}{\left(2x+1\right)^4+2}< =\dfrac{3}{2}\)
Dấu = xảy ra khi 2x+1=0
=>x=-1/2

(a) \(A=\dfrac{3}{x-2}\in Z\)
\(\Rightarrow\left(x-2\right)\inƯ\left(3\right)=\left\{\pm1;\pm3\right\}\)
\(\Rightarrow\left[{}\begin{matrix}x-1=1\\x-1=-1\\x-1=3\\x-1=-3\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=2\\x=0\\x=4\\x=-2\end{matrix}\right.\)
Vậy: \(x\in\left\{-2;0;2;4\right\}.\)
(b) \(B=-\dfrac{11}{2x-3}\in Z\)
\(\Rightarrow\left(2x-3\right)\inƯ\left(11\right)=\left\{\pm1;\pm3\right\}\)
\(\Rightarrow\left[{}\begin{matrix}2x-3=1\\2x-3=-1\\2x-3=11\\2x-3=-11\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=2\\x=1\\x=7\\x=-4\end{matrix}\right.\)
Vậy: \(x\in\left\{-4;1;2;7\right\}.\)
(c) \(C=\dfrac{x+3}{x+1}=\dfrac{\left(x+1\right)+2}{x+1}=1+\dfrac{2}{x+1}\in Z\Rightarrow\dfrac{2}{x+1}\in Z\)
\(\Rightarrow\left(x+1\right)\inƯ\left(2\right)=\left\{\pm1;\pm2\right\}\)
\(\Rightarrow\left[{}\begin{matrix}x+1=1\\x+1=-1\\x+1=2\\x+1=-2\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-2\\x=1\\x=-3\end{matrix}\right.\)
Vậy: \(x\in\left\{-3;-2;0;1\right\}.\)
(d) \(D=\dfrac{2x+10}{x+3}=\dfrac{2\left(x+3\right)+4}{x+3}=2+\dfrac{4}{x+3}\in Z\Rightarrow\dfrac{4}{x+3}\in Z\)
\(\Rightarrow\left(x+3\right)\inƯ\left(4\right)=\left\{\pm1;\pm2\pm4\right\}\)
\(\Rightarrow x\in\left\{-2;-4;-1;-5;1;-7\right\}\)


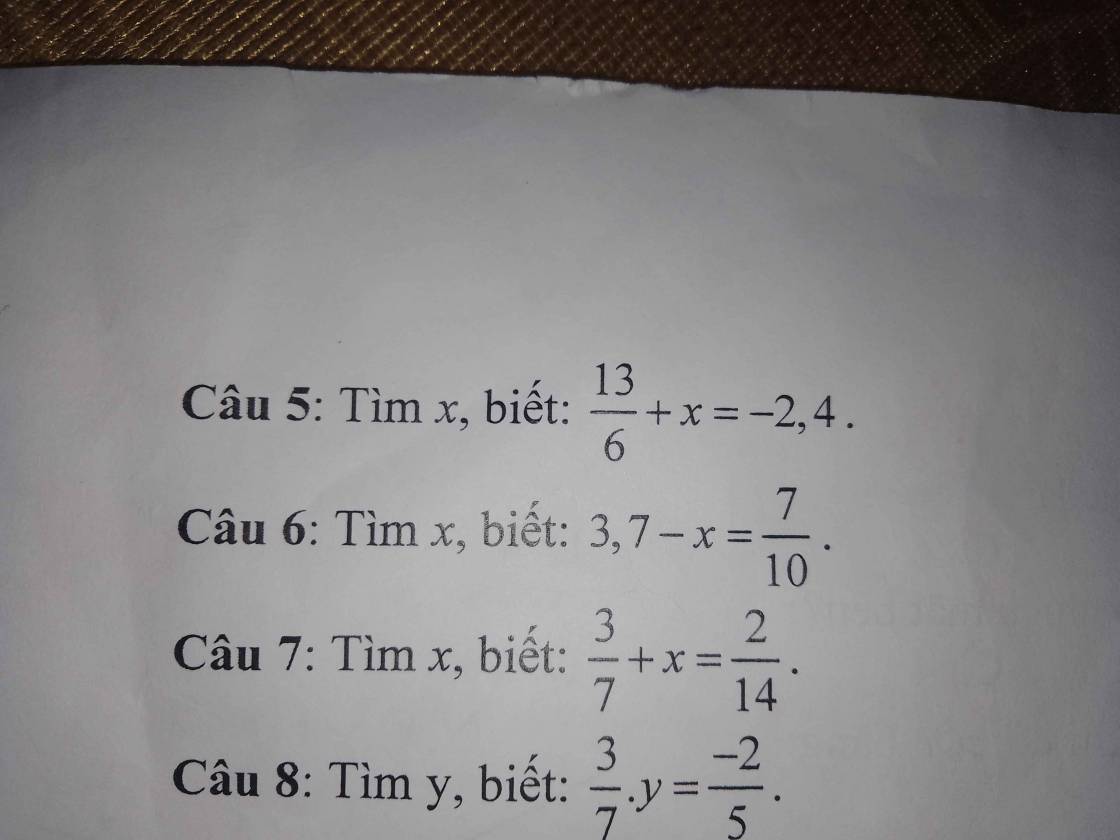
 ai giải giúp em từ 3 đến bài 12 với ạ em đang cần gấp chiều em đi thi ạ
ai giải giúp em từ 3 đến bài 12 với ạ em đang cần gấp chiều em đi thi ạ


 giúp em với ạ em đang cần gấp ạ
giúp em với ạ em đang cần gấp ạ giúp em với ạ em đang cần gấp ạ :(
giúp em với ạ em đang cần gấp ạ :(

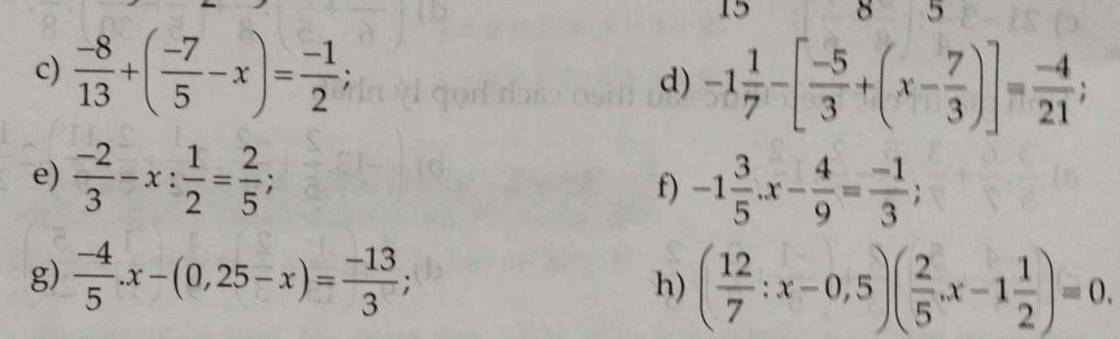
 giúp em với ạ em đang cần gấp ạ. Bài nào làm đc trc thì làm trc giúp em với ạ
giúp em với ạ em đang cần gấp ạ. Bài nào làm đc trc thì làm trc giúp em với ạ giúp em với ạ em đang cần gấp lắm ạ em cảm ơn trước
giúp em với ạ em đang cần gấp lắm ạ em cảm ơn trước
a: Xét ΔBAM vuông tại A và ΔBKM vuông tại K có
BM chung
\(\widehat{ABM}=\widehat{KBM}\)
Do đó: ΔBAM=ΔBKM
=>BA=BK
=>ΔBAK cân tại B
b: Ta có: \(\widehat{CAK}+\widehat{BAK}=\widehat{BAC}=90^0\)
\(\widehat{DAK}+\widehat{BKA}=90^0\)(ΔDAK vuông tại D)
mà \(\widehat{BAK}=\widehat{BKA}\)(ΔBAK cân tại B)
nên \(\widehat{CAK}=\widehat{DAK}\)
=>AK là phân giác của góc DAC
c: Xét ΔABC vuông tại A có AD là đường cao
nên \(AD\cdot BC=AB\cdot AC\)
\(\left(AB+AC\right)^2-\left(BC+AD\right)^2\)
\(=AB^2+AC^2+2\cdot AB\cdot AC-BC^2-2\cdot BC\cdot AD-AD^2\)
\(=BC^2+2\cdot BC\cdot AD-BC^2-2\cdot BC\cdot AD-AD^2\)
\(=-AD^2< 0\)
=>\(\left(AB+AC\right)^2< \left(BC+AD\right)^2\)
=>AB+AC<BC+AD