
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




2:
1+cot^2a=1/sin^2a
=>1/sin^2a=1681/81
=>sin^2a=81/1681
=>sin a=9/41
=>cosa=40/41
tan a=1:40/9=9/40


2x2 - ( m + 4 )x + m = 0
Δ = b2 - 4ac = ( m + 4 )2 - 8m = m2 + 8m + 16 - 8m = m2 + 16
Vì m2 + 16 ≥ 16 > 0 ∀ m => Δ ≥ 16 > 0
Vậy phương trình luôn có nghiệm ( đpcm )


\(\Leftrightarrow n^5+n^2-n^2+1⋮n^3+1\)
\(\Leftrightarrow-n^3+n⋮n^3+1\)
\(\Leftrightarrow n=1\)

Bài 2: ĐKXĐ: \(x\notin\left\{3;-3\right\}\)
\(\Leftrightarrow\dfrac{6}{\left(x-3\right)\left(x+3\right)}=\dfrac{x^2-9+x+3}{\left(x-3\right)\left(x+3\right)}\)
Suy ra: \(x^2+x-12=0\)
\(\Leftrightarrow\left(x+4\right)\left(x-3\right)=0\)
=>x=-4(nhận) hoặc x=3(loại)
Bài 1:
a,ĐKXĐ:\(\left\{{}\begin{matrix}\sqrt{a}+1\ne0\left(luôn.đúng\right)\\\sqrt{a}-5\ne0\end{matrix}\right.\Leftrightarrow\sqrt{a}\ne5\Leftrightarrow a\ne25\)
\(b,A=\left(3+\dfrac{a+\sqrt{a}}{\sqrt{a}+1}\right)\left(3-\dfrac{a-5\sqrt{a}}{\sqrt{a}-5}\right)\)
\(\Rightarrow A=\left(3+\dfrac{\sqrt{a}\left(\sqrt{a}+1\right)}{\sqrt{a}+1}\right)\left(3-\dfrac{\sqrt{a}\left(\sqrt{a}-5\right)}{\sqrt{a}-5}\right)\)
\(\Rightarrow A=\left(3+\sqrt{a}\right)\left(3-\sqrt{a}\right)\)
\(\Rightarrow A=9-a\)

Lấy \(2.\left(2\right)-\left(1\right)\) ta được:
\(2b+4a+6-\left(a-1-2b\right)=0\)
\(\Leftrightarrow4b+3a+7=0\Rightarrow b=\dfrac{-3a-7}{4}\)
Thế vào (2):
\(\sqrt{a^2+\left(\dfrac{-3a-7}{4}\right)^2}=\dfrac{-3a-7}{4}+2a+3\)
\(\Leftrightarrow\sqrt{25a^2+42a+49}=5a+5\) (\(a\ge-1\))
\(\Leftrightarrow25a^2+42a+49=25a^2+50a+25\)
\(\Rightarrow a=...\Rightarrow b=...\)







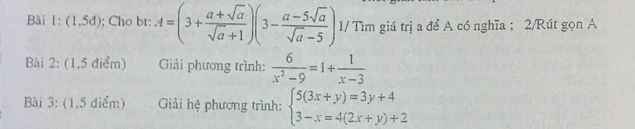

số học sinh lớp 9A là x
số khẩu trang mỗi học sinh đc phát là \(\frac{19}{x}\)
số học sinh thực tế nhận khẩu trang là x-8
số khẩu trang phát mỗi học sinh đc phát thực tế là \(\frac{19}{x-8}\)
ta có pt
\(\frac{19}{x-8}-\frac{19}{x}=2\)
\(19x-19x+152=2x\left(x-8\right)\)
\(152=2x^2-16x\)
\(2x^2-16x-152=0\)
\(a=2,b=-16,c=-152\)
\(\Delta=256-4.2.\left(-152\right)=1472\)
\(\Delta>0\)<=> có 2 n0 pb
\(\sqrt{\Delta}=8\sqrt{23}\)
\(x_1=\frac{16+8\sqrt{23}}{4}\left(ktm\right)\)
\(x_2=\frac{16-8\sqrt{23}}{4}\left(ktm\right)\)
vậy ko có giá trị nào tm yêu cầu đề bài
bạn chụp lại toàn bài cho mình nha ko mình ko biết là có phải nhà trường cấp 19 khẩu trang ko nữa