Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
ta co tam giac ANM dong dang voi tam giac ABC
goc A chung
AN/AB=AM/AC
suy ra AN/AB=MN/BC
thay so do vao
MN=8*18/12=12cm
Ta có: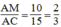 
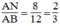
Suy ra: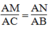 
Xét ΔABC và ΔANM, ta có
+ Góc A chung
+ 
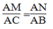
Suy ra:
△
ANM đồng dạng
△
ABC(c.g.c) ⇒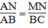 
Vậy MN =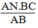 
= (8.18)/12 = 12 cm
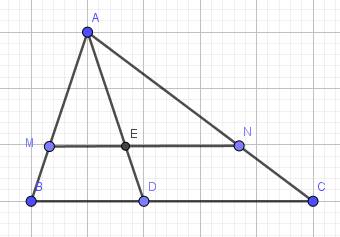
\(\Delta ABC\) có:
\(\dfrac{AM}{AB}=\dfrac{8}{12}=\dfrac{2}{3}\)
\(\dfrac{AN}{AC}=\dfrac{12}{15}=\dfrac{2}{3}\)
\(\Rightarrow\dfrac{AM}{AB}=\dfrac{AN}{AC}=\dfrac{2}{3}\)
\(\Rightarrow\) MN // BC (định lý Ta-lét)
\(\Delta AME\) và \(\Delta ABD\) có:
ME // BD (do MN // BC)
\(\Rightarrow\dfrac{AE}{AD}=\dfrac{AM}{AB}=\dfrac{2}{3}\) (hệ quả của định lý Ta-lét)
a) Do MN//BC nên theo hệ quả của ĐL Ta-let ta có \(\dfrac{AM}{AB}\)=\(\dfrac{MN}{BC}\)
\(\Rightarrow\) \(\dfrac{2}{4}\) = \(\dfrac{MN}{6}\)\(\Rightarrow\) MN = \(\dfrac{2\times6}{4}\)\(\Rightarrow\) MN = 3 cm
b) Do MN//BC nên theo ĐL Ta-let ta có \(\dfrac{AM}{AB}\)=\(\dfrac{AN}{AC}\)
\(\Rightarrow\)\(\dfrac{12}{15}\)=\(\dfrac{AN}{18}\)\(\Rightarrow\) AN = \(\dfrac{12\times18}{15}\) = 14,4 cm
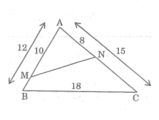
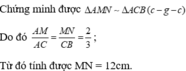
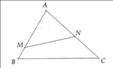
Xét \(\Delta\)ABC và \(\Delta\)ANM ta có:
A:góc chung
\(\frac{AN}{AB}\)=\(\frac{AM}{AC}=\frac{2}{3}\)
=> \(\Delta\)ABC và \(\Delta\)ANM đồng dạng
=>\(\frac{MN}{BC}=\frac{AN}{AB}\)
=>\(MN=\frac{AN.BC}{AB}=\frac{8.18}{12}=12\)