Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta dùng lệnh Solutions(<Phương trình>) trên ô lệnh của cửa sổ CAS, kết quả sẽ hiển thị ngay bên dưới:
a)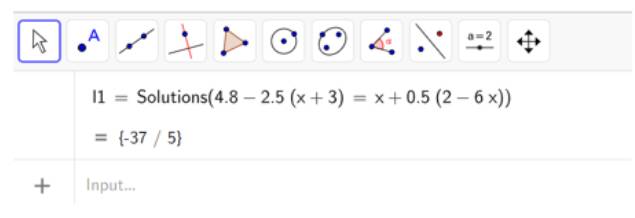
Vậy phương trình đã cho có duy nhất nghiệm \(x=-\dfrac{37}{5}\)
b)
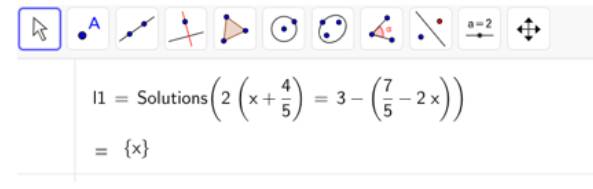
Vậy phương trình đã cho có vô số nghiệm.

a) Đây là kết luận đúng vì: \( - 6.2{y^2} = - 3y.4y\)
b) Đây là kết luận đúng vì: \(5{\rm{x}}\left( {x + 3} \right) = 5\left( {{x^2} + 3{\rm{x}}} \right) = 5{{\rm{x}}^2} + 15{\rm{x}}\)
c) Đây là kết luận đúng vì: \(3{\rm{x}}\left( {4{\rm{x}} + 1} \right)\left( {1 - 4{\rm{x}}} \right) = 3{\rm{x}}\left( {1 - 16{{\rm{x}}^2}} \right) = - 3{\rm{x}}\left( {16{{\rm{x}}^2} - 1} \right)\)

a) ĐKXĐ: x khác +2
\(\frac{x-2}{2+x}-\frac{3}{x-2}-\frac{2\left(x-11\right)}{x^2-4}\)
<=> \(\frac{x-2}{2+x}-\frac{3}{x-2}=\frac{2\left(x-11\right)}{\left(x-2\right)\left(x+2\right)}\)
<=> (x - 2)^2 - 3(2 + x) = 2(x - 11)
<=> x^2 - 4x + 4 - 6 - 3x = 2x - 22
<=> x^2 - 7x - 2 = 2x - 22
<=> x^2 - 7x - 2 - 2x + 22 = 0
<=> x^2 - 9x + 20 = 0
<=> (x - 4)(x - 5) = 0
<=> x - 4 = 0 hoặc x - 5 = 0
<=> x = 4 hoặc x = 5
làm nốt đi

Khẳng định C là khẳng định sai vì:
Nếu: \(\frac{{x + 1}}{{x - 1}} = \frac{{{x^2} + x + 1}}{{{x^2} - x + 1}}\)
\(\begin{array}{l} \Rightarrow \frac{{x + 1}}{{x - 1}} - \frac{{{x^2} + x + 1}}{{{x^2} - x + 1}} = 0\\ \Rightarrow \frac{{\left( {x + 1} \right)\left( {{x^2} - x + 1} \right) - \left( {{x^2} + x + 1} \right)\left( {x - 1} \right)}}{{\left( {x - 1} \right)\left( {{x^2} - x + 1} \right)}} = 0\\ \Rightarrow \frac{{\left( {{x^3} + 1} \right) - \left( {{x^3} - 1} \right)}}{{\left( {x - 1} \right)\left( {{x^2} - x + 1} \right)}} = \frac{2}{{\left( {x - 1} \right)\left( {{x^2} - x + 1} \right)}} = 0\end{array}\)
\( \Rightarrow \) vô lý

\(a)\left( { - \frac{{3{\rm{x}}}}{{5{\rm{x}}{y^2}}}} \right):\left( { - \frac{{5{y^2}}}{{12{\rm{x}}y}}} \right) = \frac{{ - 3{\rm{x}}}}{{5{\rm{x}}{y^2}}}.\frac{{ - 12{\rm{x}}y}}{{5{y^2}}} = \frac{{36{{\rm{x}}^2}y}}{{25{\rm{x}}{y^4}}}\)
b) \(\frac{4{{\text{x}}^{2}}-1}{8{{\text{x}}^{3}}-1}:\frac{4{{\text{x}}^{2}}+4\text{x}+1}{4{{\text{x}}^{2}}+2\text{x}+1}=\frac{4{{\text{x}}^{2}}-1}{8{{\text{x}}^{3}}-1}.\frac{4{{\text{x}}^{2}}+2\text{x}+1}{4{{\text{x}}^{2}}+4\text{x}+1}\)
\(=\frac{\left( 2\text{x}-1 \right)\left( 2\text{x}+1 \right)\left( 4{{\text{x}}^{2}}+2\text{x}+1 \right)}{\left( 2\text{x}-1 \right)\left( 4{{\text{x}}^{2}}+2\text{x}+1 \right){{\left( 2\text{x}+1 \right)}^{2}}}=\frac{1}{2\text{x}+1}\).

\(\begin{array}{l}a)\frac{{4{\rm{x}} - 6}}{{5{{\rm{x}}^2} - x}}.\frac{{25{{\rm{x}}^2} - 10{\rm{x}} + 1}}{{27 + 8{{\rm{x}}^3}}}\\ = \frac{{ - 2\left( {3 - 2{\rm{x}}} \right)}}{{x\left( {5{\rm{x}} - 1} \right)}}.\frac{{{{\left( {5{\rm{x}} - 1} \right)}^2}}}{{\left( {3 - 2{\rm{x}}} \right)\left( {9 + 6{\rm{x}} + 4{{\rm{x}}^2}} \right)}}\\ = \frac{{ - 2\left( {5{\rm{x}} - 1} \right)}}{{x\left( {9 + 6{\rm{x}} + 4{{\rm{x}}^2}} \right)}}\\b)\frac{{2{\rm{x}} + 10}}{{{{\left( {x - 3} \right)}^2}}}:\frac{{{{\left( {x + 5} \right)}^3}}}{{{x^2} - 9}}\\ = \frac{{2{\rm{x}} + 10}}{{{{\left( {x - 3} \right)}^2}}}.\frac{{{x^2} - 9}}{{{{\left( {x + 5} \right)}^2}}}\\ = \frac{{2\left( {x + 5} \right)\left( {x - 3} \right)\left( {x + 3} \right)}}{{{{\left( {x - 3} \right)}^2}{{\left( {x + 5} \right)}^3}}}\\ = \frac{{2\left( {x + 3} \right)}}{{\left( {x - 3} \right){{\left( {x + 5} \right)}^2}}}\end{array}\)

d: =>4x+6=15x-12
=>4x-15x=-12-6=-18
=>-11x=-18
hay x=18/11
e: =>\(45x+27=12+24x\)
=>21x=-15
hay x=-5/7
f: =>35x-5=96-6x
=>41x=101
hay x=101/41
g: =>3(x-3)=90-5(1-2x)
=>3x-9=90-5+10x
=>3x-9=10x+85
=>-7x=94
hay x=-94/7

`7x -(2x+3) =5(x-2)`
`<=> 7x-2x-3=5x-10`
`<=> 7x-2x-5x=-10+3`
`<=> 0x=-7` ( vô lí )
Vậy phương trình vô nghiệm
\(x+\dfrac{2x-1}{5}=3+\dfrac{3-x}{4}\\ \Leftrightarrow\dfrac{20x}{20}+\dfrac{4\left(2x-1\right)}{20}=\dfrac{3\cdot20}{20}+\dfrac{5\left(3-x\right)}{20}\\ \Leftrightarrow20x+8x-4=60+15-5x\)
`<=> 20x+8x +5x = 60+15+4`
`<=> 33x= 79`
`<=> x= 79/33`
Vậy \(S=\left\{\dfrac{79}{33}\right\}\)
a) 7x−(2x+3)=5(x−2)
7x−2x−3=5x−10
0x=−7 (không thỏa mãn điều kiện a≠0)
b) x + \(\frac{{2{\rm{x}} - 1}}{5}\)=3 + \(\frac{{3 - x}}{4}\)
\(\frac{{20{\rm{x}} + 4\left( {2{\rm{x}} - 1} \right)}}{{20}} = \frac{{15 + 5\left( {3 - x} \right)}}{{20}}\)
20x+4(2x−1)=60+5(3−x)
20x+8x−4=60+15−5x
20x+8x+5x=60+15+4
33x=79
\(x = \frac{{79}}{{33}}\)
Vậy nghiệm của phương trình là \(x = \frac{{79}}{{33}}\)
a) 5(x−1)−(6−2x)=8x−3
=>5x−5−6+2x=8x−3
=> −x=8
=> x=−8
Vậy phương trình có nghiệm là x = -8
b)
\(\begin{array}{l}\frac{{2{\rm{x}} - 1}}{3} - \frac{{5 - 3{\rm{x}}}}{2} = \frac{{x + 7}}{4}\\\frac{{4\left( {2{\rm{x}} - 1} \right)}}{{12}} - \frac{{6\left( {5 - 3{\rm{x}}} \right)}}{{12}} = \frac{{3\left( {x + 7} \right)}}{{12}}\\8{\rm{x}} - 4 - 30 + 18{\rm{x}} = 3{\rm{x}} + 21\\8{\rm{x + 18x}} - 3{\rm{x}} = 21 + 4 + 30\\23{\rm{x}} = 55\\x = \frac{{55}}{{23}}\end{array}\)
Vậy phương trình có nghiệm là \(x = \frac{{55}}{{23}}\)