K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
9 tháng 4 2022
a: Xét ΔABE và ΔHBE có
BA=BH
\(\widehat{ABE}=\widehat{HBE}\)
BE chung
Do đó: ΔABE=ΔHBE
b: Ta có: ΔABE=ΔHBE
nên BA=BH và EA=EH
=>BE là đường trung trực của AH
d: ta có: EA=EH
mà EH<EC
nên EA<EC
NB
1
29 tháng 7 2023
a: BC=căn 6^2+8^2=10cm
b: Xét ΔBAI vuông tại A và ΔBHI vuông tại H có
BI chung
góc ABI=góc HBI
=>ΔBAI=ΔBHI
=>IA=IH
mà IH<IC
nên IA<IC
c: Xét ΔIAK vuông tại A và ΔIHC vuông tại H có
IA=IH
góc AIK=góc HIC
=>ΔIAK=ΔIHC
=>AK=HC
d: Xét ΔBKC có BA/AK=BH/HC
nên AH//KC
19 tháng 2 2022
Bài 2: Chọn C
Bài 4:
a: \(\widehat{C}=180^0-80^0-50^0=50^0\)
Xét ΔABC có \(\widehat{A}=\widehat{C}< \widehat{B}\)
nên BC=AB<AC
b: Xét ΔABC có AB<BC<AC
nên \(\widehat{C}< \widehat{A}< \widehat{B}\)
TH
1
26 tháng 2 2022
a: Xét ΔABC có
M là trung điểm của BC
MP//AC
DO đó: P là trung điểm của AB
hay PA=PB
b: Xét ΔABC có
M là trung điểm của BC
MN//AB
Do đó: N là trung điểm của AC
Xét ΔABC có
P là trung điểm của AB
N là trung điểm của AC
Do đó: PN là đường trung bình
=>PN//BC
NN
4
17 tháng 4 2023
Chứng tỏ rằng đa thức \(x^{2008}-x^{2007}+1\) vô nghiệm hay gì vậy ạ :v?
24 tháng 8 2017
ta có: a+b+c=1
<=>(a+b+c)^2=1
<=>ab+bc+ca=0 (1)
mặt khác: áp dụng tính chất dãy tỉ số bằng nhau ta có:
x/a=y/b=z/c=(x+y+z)/(a+b+c)=x+y+z
<=> x=a(x+y+z) ; y=b(x+y+z) ; z=c(x+y+z)
=>xy+yz+zx=ab(x+y+z)^2+bc(x+y+z)^2+ca(x...
<=>xy+yz+zx=(ab+bc+ca)(x+y+z)^2 (2)
từ (1) và (2) ta có đpcm
NT
1
5 tháng 4 2023
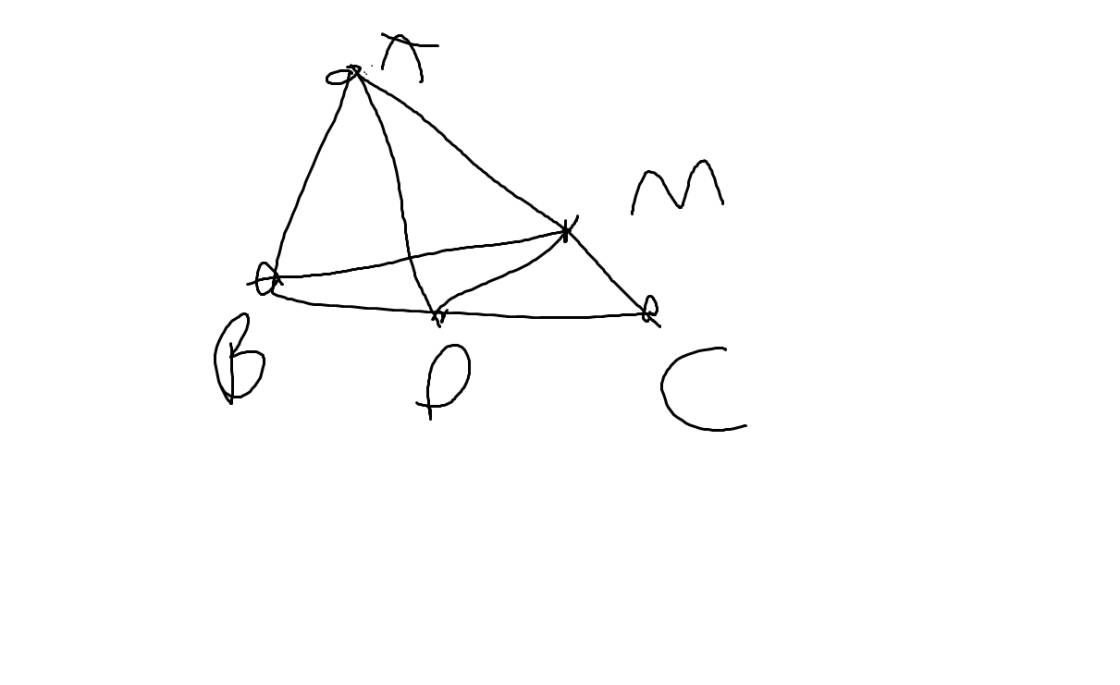
ΔAED vuông tại E nên AE<AD
ΔDFC vuông tại F nên FC<DC
=>AE+FC<AD+DC=AC
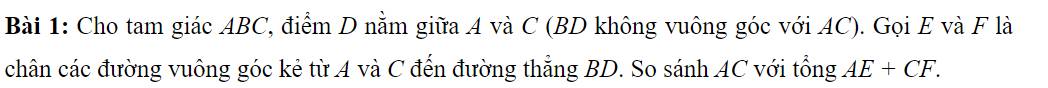
a: Ta có: \(\widehat{HAC}+\widehat{ACB}=90^0\)(ΔAHC vuông tại H)
\(\widehat{ABC}+\widehat{ACB}=90^0\)(ΔABC vuông tại A)
Do đó: \(\widehat{HAC}=\widehat{ABC}\)
b: Ta có: \(\widehat{CAK}+\widehat{BAK}=\widehat{BAC}=90^0\)
\(\widehat{CKA}+\widehat{HAK}=90^0\)(ΔHAK vuông tại H)
mà \(\widehat{BAK}=\widehat{HAK}\)(AK là phân giác của góc HAB)
nên \(\widehat{CAK}=\widehat{CKA}\)
c: Xét ΔCAK có \(\widehat{CAK}=\widehat{CKA}\)
nên ΔCAK cân tại C
ΔCAK cân tại C
mà CP là đường phân giác
nên CP\(\perp\)AK