
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: góc ABC=90 độ-góc ACB
góc KHC=90 độ-góc ACB
=>góc ABC=góc KHC
b: Xét ΔBAH vuông tại A và ΔBKH vuông tại K có
BH chung
góc ABH=góc KBH
=>ΔBAH=ΔBKH
=>BA=BK và HA=HK
=>BH là trung trực của AK
c: Xét ΔIBC có
BD,CA là đường cao
BD căt CAt tại H
=>H là trực tâm
=>I,H,K thẳng hàng
d: ΔADK đều
=>góc ADH=30 độ
=>góc AIK=30 độ
=>góc ABC=60 độ

a: Xét ΔBAD có BA=BD
nên ΔBAD cân tại B
hay \(\widehat{BAD}=\widehat{BDA}\)
b: \(\widehat{HAD}+\widehat{BDA}=90^0\)
\(\widehat{CAD}+\widehat{BAD}=90^0\)
mà \(\widehat{BAD}=\widehat{BDA}\)
nên \(\widehat{HAD}=\widehat{CAD}\)
hay AD là tia phân giác của góc HAC
c: Xét ΔADH vuông tại H và ΔADK vuông tại K có
AD chung
\(\widehat{HAD}=\widehat{KAD}\)
Do đó:ΔADH=ΔADK
Suy ra: AH=AK

\(x^3+2x^2\left(4y-1\right)-4xy^2-9y^3-f\left(x\right)=-5x^3+8x^2y-4xy^2-9y^3\\ \Rightarrow\left(x^3+8x^2y+2x^2-4xy^2-9y^3\right)-f\left(x\right)=-5x^3+8x^2y-4xy^2-9y^3\\ \Rightarrow f\left(x\right)=x^3+8x^2y+2x^2-4xy^2-9y^3+5x^3-8x^2y+4xy^2+9y^3\\ \Rightarrow f\left(x\right)=6x^3+2x^2\)

a) \(\Rightarrow\left|\dfrac{3}{4}+x\right|=0\Rightarrow\dfrac{3}{4}+x=0\Rightarrow x=-\dfrac{3}{4}\)
b) \(\Rightarrow x+0,4=\dfrac{4}{9}:\dfrac{2}{3}=\dfrac{2}{3}\Rightarrow x=\dfrac{2}{3}-0,4=\dfrac{4}{15}\)

Đề trước đó:

(x-7)(x+1)-(x-3)^2=(3x-5)(3x+5)-(3x+1)^2+(x-2)^2-x
<=>x^2+x-7x-7-x^2+6x-9=9x^2-25-9x^2-6x-1+x^2-4x+4-x
<=>x^2-11x-6=0
<=>x^2-2x. 11/2 + 121/4-145/4=0
<=>(x-11/2)^2=145/4
<=>|x-11/2|=căn(145)/2
<=>x=[11+-căn(145)]/2

a: \(=\left(2a^2-3a^2-4a^2\right)+\left(-0.5a-2.5a+3a\right)+\left(5-4+7\right)=-5a^2+8\)
b: \(=\left(a^3-a^3\right)+\left(-2a^2-3a^2+4a^2\right)+\left(a+a-a\right)+\left(-5+4\right)=-a^2+a-1\)
c: \(=-b^4+3b^2-3b-1-b^3+1-3b^2+b^4-5+4b^3+5\)
\(=3b^3-3b\)

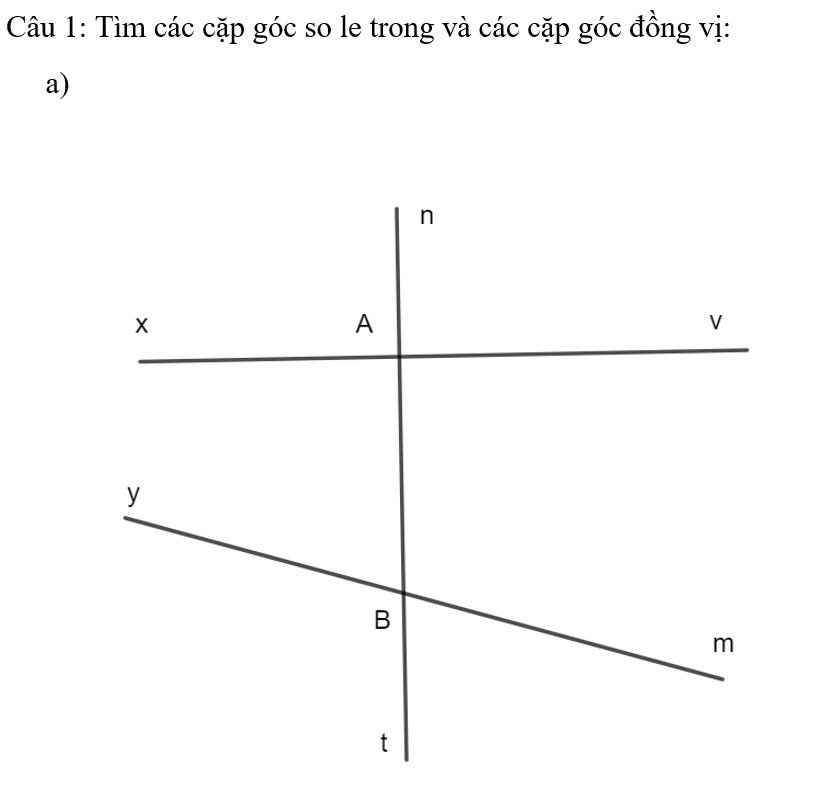
a: So le trong: góc vAB và góc yBA; góc xAB và góc mBA
ĐỒng vị: góc nAx và góc yBA; góc nAv và góc mBA; góc xAB và góc tBy; góc vAB và góc mBt
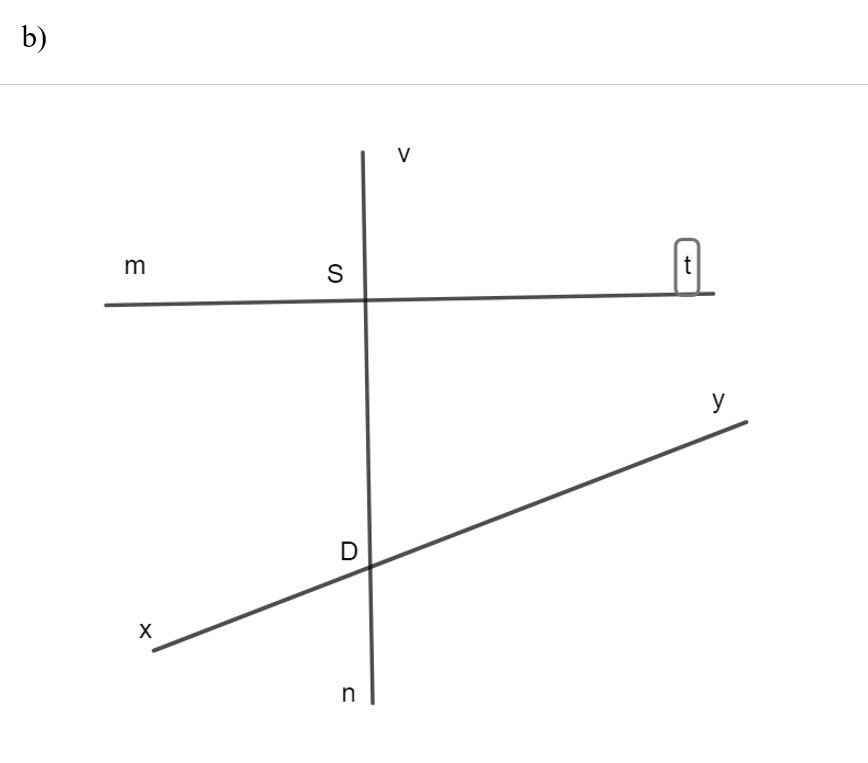
b: So le trong: góc mSD và góc yDS; góc tSD và góc xDS
ĐỒng vị: góc vSm và góc xDv; góc vSt và góc vDy; góc mSn và góc xDn; góc tSD và góc yDn
a)Cặp so le trong: xAB và ABm, vAB và ABy
Cặp đồng vị: nAx và ABy, nAv và ABm, xAB và yBt,vAB và mBt
b)Cặp so le trong: mSD và SDy, tSD và SDx
Cặp đồng vị: vSm và SDx, vSt và SDy, nDx và DSm,nDy và DSt

1: A=-1/2*xy^3*4x^2y^2=-2x^3y^5
Bậc là 8
Phần biến là x^3;y^5
Hệ số là -2
2:
a: P(x)=3x+4x^4-2x^3+4x^2-x^4-6
=3x^4-2x^3+4x^2+3x-6
Q(x)=2x^4+4x^2-2x^3+x^4+3
=3x^4-2x^3+4x^2+3
b: A(x)=P(x)-Q(x)
=3x^4-2x^3+4x^2+3x-6-3x^4+2x^3-4x^2-3
=3x-9
A(x)=0
=>3x-9=0
=>x=3
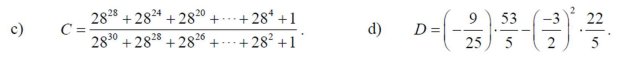
 Giúp mình với các bạn,mình cần gấp câu c1 và câu d2 ạ !
Giúp mình với các bạn,mình cần gấp câu c1 và câu d2 ạ !

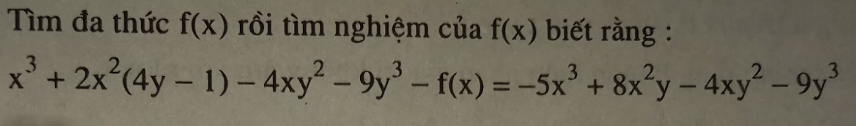

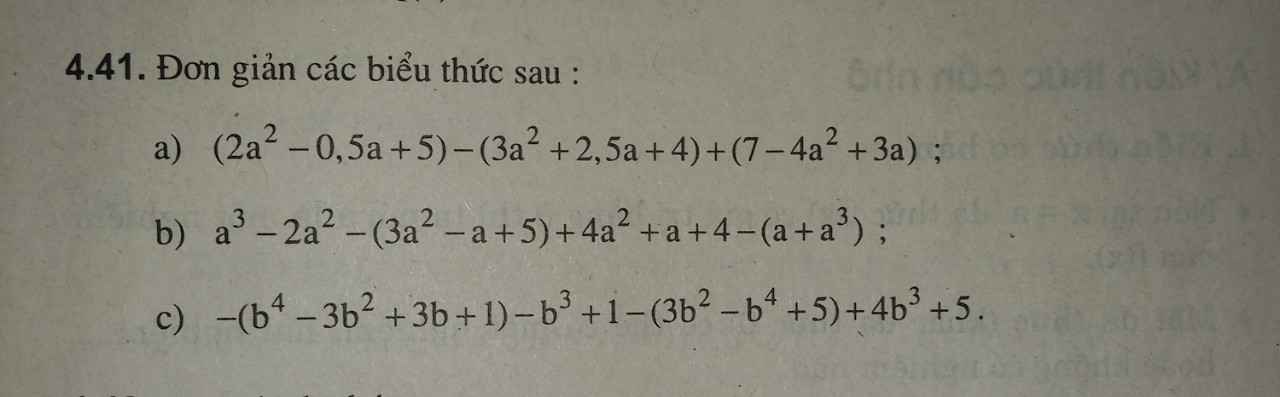

c; C = \(\dfrac{28^{28}+28^{24}+...+28^4+1}{28^{30}+28^{28}+...+28^2+1}\)
A = 1 + 284 + 288 + 2812 + ...2828
284A = 284 + 288 + 2812 + ... + 2828 + 2832
284A - A = 284+ 288+...+2828+ 2832- (1 + 284 + 288+...+2828)
(284 - 1)A = 284 + 288+ ...+ 2828 + 2832 - 1 - 284- ...- 2828
(284 - 1)A = (2832 - 1) + (284 - 284) + (288 - 288) + ... + (2828 - 2828)
(284 - 1)A = 2832 - 1 + 0 + 0... + 0
A = (2832 - 1): (284 - 1)
Đặt B = 2830 + 2828 + ... + 282 + 1
282B = 2832 + 2830 + ... + 284 + 282
282B - B = 2832 + 2830 + ... + 284 + 282 - (2830 + 2828 +...+1)
(282 - 1)B = 2832 + 2830+...+284 + 282 - 2830 - 2828 - ... 282- 1
(282 - 1)B = (2832 - 1) + (2830 - 2830) +...+(282 - 282)
(282 - 1)B = (2832 - 1) + 0 + 0 +...+ 0
(282 - 1)B = 2832 - 1
B = (2832 - 1): (282 - 1)
C = \(\dfrac{A}{B}\) = \(\dfrac{28^{32}-1}{28^4-1}\) : \(\dfrac{28^{32}-1}{28^2-1}\)
C = \(\dfrac{28^{32}-1}{28^4-1}\) \(\times\) \(\dfrac{28^2-1}{28^{32}-1}\)
C = \(\dfrac{28^2-1}{28^4-1}\)
C = \(\dfrac{1}{785}\)
Câu d:
\(\dfrac{x-1}{99}\) + \(\dfrac{x-2}{98}\) + \(\dfrac{x-3}{97}\) = \(\dfrac{x-4}{96}\) + \(\dfrac{x-5}{95}\) + \(\dfrac{x-6}{94}\)
(\(\dfrac{x-1}{99}\)-1)+(\(\dfrac{x-2}{98}\)-1)+(\(\dfrac{x-3}{97}\)-1) = (\(\dfrac{x-4}{96}\)-1) + (\(\dfrac{x-5}{95}\)-1)+(\(\dfrac{x-6}{94}\)-1)
\(\dfrac{x-100}{99}\)+\(\dfrac{x-100}{98}\)+\(\dfrac{x-100}{97}\) = \(\dfrac{x-100}{96}\)+\(\dfrac{x-100}{95}\)+\(\dfrac{x-100}{94}\)
\(\dfrac{x-100}{99}\)+\(\dfrac{x-100}{98}\)+\(\dfrac{x-100}{97}\)- \(\dfrac{x-100}{96}\)-\(\dfrac{x-100}{95}\)-\(\dfrac{x-100}{94}\) = 0
(\(x-100\)).(\(\dfrac{1}{99}\)+\(\dfrac{1}{98}\)+\(\dfrac{1}{97}\) - \(\dfrac{1}{96}\)-\(\dfrac{1}{95}\)-\(\dfrac{1}{94}\)) = 0
Vì\(\dfrac{1}{98}< \dfrac{1}{98}< \dfrac{1}{97}< \dfrac{1}{96}< \dfrac{1}{95}< \dfrac{1}{94}\)
Nên (\(\dfrac{1}{99}\) + \(\dfrac{1}{98}\) + \(\dfrac{1}{97}\) )- (\(\dfrac{1}{96}\) + \(\dfrac{1}{95}\) +\(\dfrac{1}{94}\) )< 0
⇒\(x-100\) = 0
Vậy \(x\) = 100