
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(M=\left(\dfrac{a-1}{2\sqrt{a}}\right)^2\cdot\dfrac{a-2\sqrt{a}+1-a-2\sqrt{a}-1}{\left(\sqrt{a}-1\right)\left(\sqrt{a}+1\right)}\\ M=\dfrac{\left(a-1\right)^2}{4a}\cdot\dfrac{-4\sqrt{a}}{a-1}=\dfrac{1-a}{\sqrt{a}}\)
anh có thể ghi thêm các bước trước khi ra đc mấy cái này ko ạ tại rút gọn quá e ch hỉu ạ e c.ơn

b: Tọa độ là:
\(\left\{{}\begin{matrix}\dfrac{2}{3}x=-\dfrac{1}{3}x+2\\y=\dfrac{2}{3}x\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=\dfrac{4}{3}\end{matrix}\right.\)

Bài 1:
a: Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=6^2+8^2=100\)
hay BC=10(cm)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot BC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}BH=3.6\left(cm\right)\\CH=6.4\left(cm\right)\end{matrix}\right.\)
b: Áp dụng hệ thức lượng trong tam giác vuông vào ΔAHB vuông tại H có HF là đường cao ứng với cạnh huyền AB, ta được:
\(AF\cdot AB=AH^2\left(1\right)\)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔAHC vuông tại H có HE là đường cao ứng với cạnh huyền AC, ta được:
\(AE\cdot AC=AH^2\left(2\right)\)
Từ (1) và (2) suy ra \(AF\cdot AB=AE\cdot AC\)

Bạn ơi, làm như vậy thì quá ngắn rồi ạ, với lại bạn làm thiếu mất đề bài của mình rồi

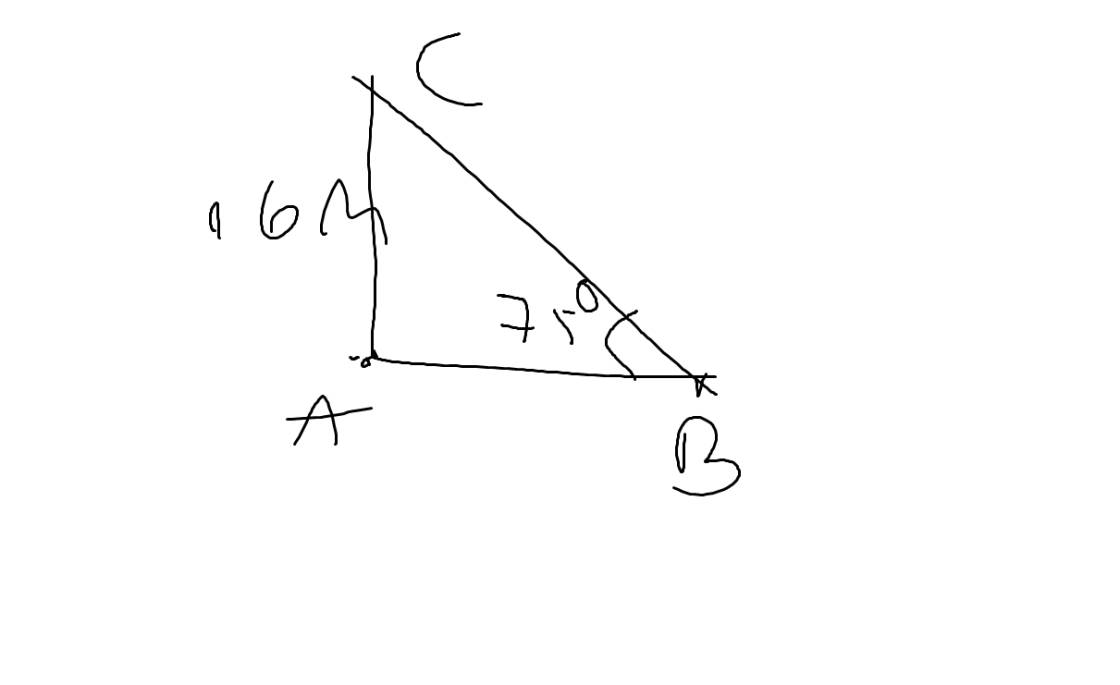
Gọi A,B lần lượt là hai mốc của bờ sông. Gọi điểm C là điểm nằm trên đường thước dây vuông góc với bờ sông tại A
=>AB vuông góc AC tại A
Theo đề, ta có: AC=16m \(\widehat{ABC}=75^0\)
Xét ΔABC vuông tại A có \(tanB=\dfrac{AC}{AB}\)
=>\(AB=\dfrac{AC}{tanB}=16:tan75\simeq4,3\left(m\right)\)

b: \(BC=\sqrt{89}\left(cm\right)\)
\(\sin\widehat{B}=\dfrac{5\sqrt{89}}{89}\)
\(\Leftrightarrow\widehat{B}\simeq32^0\)
\(\widehat{C}=58^0\)

b: Tọa độ giao điểm là:
\(\left\{{}\begin{matrix}\dfrac{2}{3}x=-\dfrac{1}{3}x+2\\y=\dfrac{2}{3}x\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=\dfrac{4}{3}\end{matrix}\right.\)

Bài IV:
1: Xét tứ giác MAOB có
\(\widehat{MAO}+\widehat{MBO}=90^0+90^0=180^0\)
=>MAOB là tứ giác nội tiếp
=>M,A,O,B cùng thuộc một đường tròn
2: Xét (O) có
MA,MB là các tiếp tuyến
Do đó: MA=MB
=>M nằm trên đường trung trực của AB(1)
Ta có: OA=OB
=>O nằm trên đường trung trực của AB(2)
Từ (1) và (2) suy ra MO là đường trung trực của BA
=>MO\(\perp\)AB tại H và H là trung điểm của AB
Xét ΔMAO vuông tại A có AH là đường cao
nên \(MH\cdot MO=MA^2\left(3\right)\)
Xét (O) có
ΔACD nội tiếp
AD là đường kính
Do đó: ΔACD vuông tại C
=>AC\(\perp\)CD tại C
=>AC\(\perp\)DM tại C
Xét ΔADM vuông tại A có AC là đường cao
nên \(MC\cdot MD=MA^2\left(4\right)\)
Từ (3) và (4) suy ra \(MA^2=MH\cdot MO=MC\cdot MD\)
3: Ta có: \(\widehat{MAI}+\widehat{OAI}=\widehat{OAM}=90^0\)
\(\widehat{HAI}+\widehat{OIA}=90^0\)(ΔAHI vuông tại H)
mà \(\widehat{OAI}=\widehat{OIA}\)
nên \(\widehat{MAI}=\widehat{HAI}\)
=>AI là phân giác của góc HAM
Xét ΔAHM có AI là phân giác
nên \(\dfrac{HI}{IM}=\dfrac{AH}{AM}\left(5\right)\)
Xét ΔOHA vuông tại H và ΔOAM vuông tại A có
\(\widehat{HOA}\) chung
Do đó: ΔOHA đồng dạng với ΔOAM
=>\(\dfrac{OH}{OA}=\dfrac{HA}{AM}\)
=>\(\dfrac{OH}{OI}=\dfrac{AH}{AM}\left(6\right)\)
Từ (5) và (6) suy ra \(\dfrac{OH}{OI}=\dfrac{IH}{IM}\)
=>\(HO\cdot IM=IO\cdot IH\)










4.
a.
Áp dụng đẳng thức: \(sin^2\alpha+cos^2\alpha=1\)
\(\Rightarrow\left(\dfrac{1}{3}\right)^2+cos^2\alpha=1\)
\(\Rightarrow cos^2\alpha=1-\left(\dfrac{1}{3}\right)^2=\dfrac{8}{9}\)
\(\Rightarrow cos\alpha=\dfrac{2\sqrt{2}}{3}\) (do \(\alpha\) nhọn nên \(cos\alpha>0\))
\(tan\alpha=\dfrac{sin\alpha}{cos\alpha}=\dfrac{1}{3}:\dfrac{2\sqrt{2}}{3}=\dfrac{\sqrt{2}}{4}\)
b.
\(P=sin^21^0+sin^289^0+sin^22^0+sin^288^0+...+sin^244^0+sin^246^0+sin^245^0+sin^290^0\)
\(=sin^21^0+sin^2\left(90^0-1^0\right)+sin^22^0+sin^2\left(90^0-2^0\right)+...+sin^244^0+sin^2\left(90^0-44^0\right)+\left(\dfrac{\sqrt{2}}{2}\right)^2+1^2\)
\(=sin^21^0+cos^21^0+sin^22^0+cos^22^0+...+sin^244^0+cos^244^0+\dfrac{3}{2}\)
\(=1+1+...+1+\dfrac{3}{2}\) (có 44 số 1)
\(=44+\dfrac{3}{2}=\dfrac{91}{2}\)
c.
\(\dfrac{1-tan\alpha}{1+tan\alpha}=\dfrac{1-\dfrac{sin\alpha}{cos\alpha}}{1+\dfrac{sin\alpha}{cos\alpha}}=\dfrac{\dfrac{cos\alpha-sin\alpha}{cos\alpha}}{\dfrac{cos\alpha+sin\alpha}{cos\alpha}}=\dfrac{cos\alpha-sin\alpha}{cos\alpha+sin\alpha}\)