Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Số hạt nhân chưa phóng xạ chính là số hạt nhân còn lại
\(N= N_0 2^{-\frac{t}{T}}= N_0 .2^{-4}= \frac{1}{16}N_0.\)

Số hạt nhân chưa bị phân rã (số hạt nhân còn lại)
\(N= N_0 2^{-\frac{t}{T}} = N_02^{-\frac{0,5T}{T}}= N_02^{-0,5}= \frac{N_0}{\sqrt{2}}.\)

@Tuấn: Do sau một chu kì thì số hạt chất phóng xạ còn một nửa. Ban đầu là N01 và N02 thì sau một chu kì còn là (N01+N02)/2

Sau khoảng thời gian \(\tau\) thì số hạt nhân còn lại là
\(N = N_0 2^{-\frac{\tau}{T}}\)
=> \(\frac{N}{N_0}= \frac{1}{4}= 2^{-2}= 2^{-\frac{\tau}{T}}\)
=> \(\tau = 2T.\)
Sau khoảng thời gian \(2\tau\) thì số hạt còn lại là
\(N_1 = N_02^{-\frac{2\tau}{T}}= N_0.2^{-\frac{4T}{T}}= \frac{1}{16}N_0\)
=> Số hạt còn lại chiếm 6,25 % số hạt ban đầu.

- So với số hạt nhân ban đầu, sau khoảng thời gian t = 2τ số hạt nhân nguyên tử của chất phóng xạ còn lại chiếm:
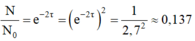

Do hạt nhân mẹ Po ban đầu đứng yên, áp dụng định luật bảo toàn động lượng trước và sau phản ứng ta thu được
\(P_{\alpha} = P_{Pb} \)
=> \(2m_{\alpha} K_{\alpha}=2m_{Pb}K_{Pb} \)
=> \( 4,0026.K_{\alpha}=205,9744.K_{Rn}.(1)\)
Áp dụng định luật bảo toàn năng lượng toàn phần có
\(K_{\alpha}+K_{Pb} = (m_t-m_s)c^2\)
=> \(K_{\alpha}+K_{Rn} = (m_{Po}-m_{\alpha}-m_{Pb})c^2= 0,0058.931,5 = 5,4027 MeV. (2)\)
Từ (1) và (2) giải hệ phương trình ta được
\(K_{\alpha} = 5,2997 MeV; K_{Pb} = 0,103 MeV. \)
=> \(v_{Pb}= \sqrt{\frac{2K_{Pb}}{m_{Pb}}} =\sqrt{\frac{2.0,103.10^6.1,6.10^{-19}}{205,9744.1,66055.10^{-27}}} = 3,06.10^5m/s.\)
Chú ý đổi đơn vị \(1 MeV = 10^6.1,6.10^{-19}J ; 1 u = 1,66055.10^{-27} kg.\)

\(H=H_02^{-\frac{t}{T}}\)
=> \(\frac{H}{H_0}=32^{-1}= 2^{-5}= 2^{-\frac{t}{T}}\)
=> \(t = 5T= 690.\)(ngày)

Đáp án A