Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đây toán lớp 9, ko phải toán 7 nha!
(O) tiếp xúc AB;AC lần lượt tại H;K
\(S_{AMN}=S_{OAM}+S_{OAN}=\frac{1}{2}OH.AM+\frac{1}{2}OK.AN=\frac{AM+AN}{2}\)
Vẽ \(MI\perp AC;I\in AC\)
Ta có: \(AM\ge MI\)
Áp dụng bất đẳng thức Côsi cho hai số không âm , ta có:
\(\frac{AM+AN}{2}\ge\sqrt{AM.AN}\)
Do đó :\(S_{AMN}\ge\sqrt{AM.AN}\ge\sqrt{MI.AN}\)
Ta có: \(S_{AMN}\ge\sqrt{2S_{AMN}}\Leftrightarrow S^2_{AMN}\ge2S_{AMN}\Leftrightarrow S_{AMN}\ge2\)
Dấu " = " xảy ra \(\Leftrightarrow I=A\Leftrightarrow MN\perp OA;\widehat{BAC}=90^0\)
Giá trị nhỏ nhất của diện tích tam giác AMN là 2

đường thằng (d) tiếp xúc với (O) tại A => D là tiếp tuyến của A
=> AM _|_ AB (tính chất tiếp tuyến) => tam giác AMB vuông A
lại có góc ANB=90o (góc nội tiếp chắn nửa đường tròn) => tam giác ANB vuông tại N
xét tam giác vuông AMB và ANB có \(\widehat{B}\)chung
=> tam giác AMB đồng dạng với tam giác ANB => \(\frac{AB}{BM}=\frac{BN}{AB}\Rightarrow AB^2=BN\cdot BM\)
mà AB=2R không đổi => AB2=4R2 không đổi => BM.BN=4R2 không đổi
b) ta có \(\widehat{AQP}=\frac{1}{2}\left(sđAB-sđAP\right)=\frac{1}{2}sđPB\)(định lý góc côc định ngoài đường tròn)
lại có \(PNB=\frac{1}{2}sđPB\)(tính chất góc nội tiếp) => \(AQP=PNB\left(=\frac{1}{2}sđPB\right)\)
hay \(\widehat{MQP}=\widehat{PNB}\)mà \(\widehat{MNP}+\widehat{PNB}=180^o\)(kề bù) => ^MQP=^MNP=1800
=> tứ giác MNPQ nội tiếp
c) áp dụng bđt Cosi cho 2 số dương ta có:
\(BM+BN\ge2\sqrt{BM\cdot BN}=2\sqrt{4R^2}=4R\)
dấu "=" xảy ra khi BM=BN <=> M trùng với N trái với giả thiết => BM+BN >4R(1)
chứng minh tương tự ta có BP+BQ >4R (2)
từ (1) và (2) => BM+BN+BP+BQ >8R (đpcm)
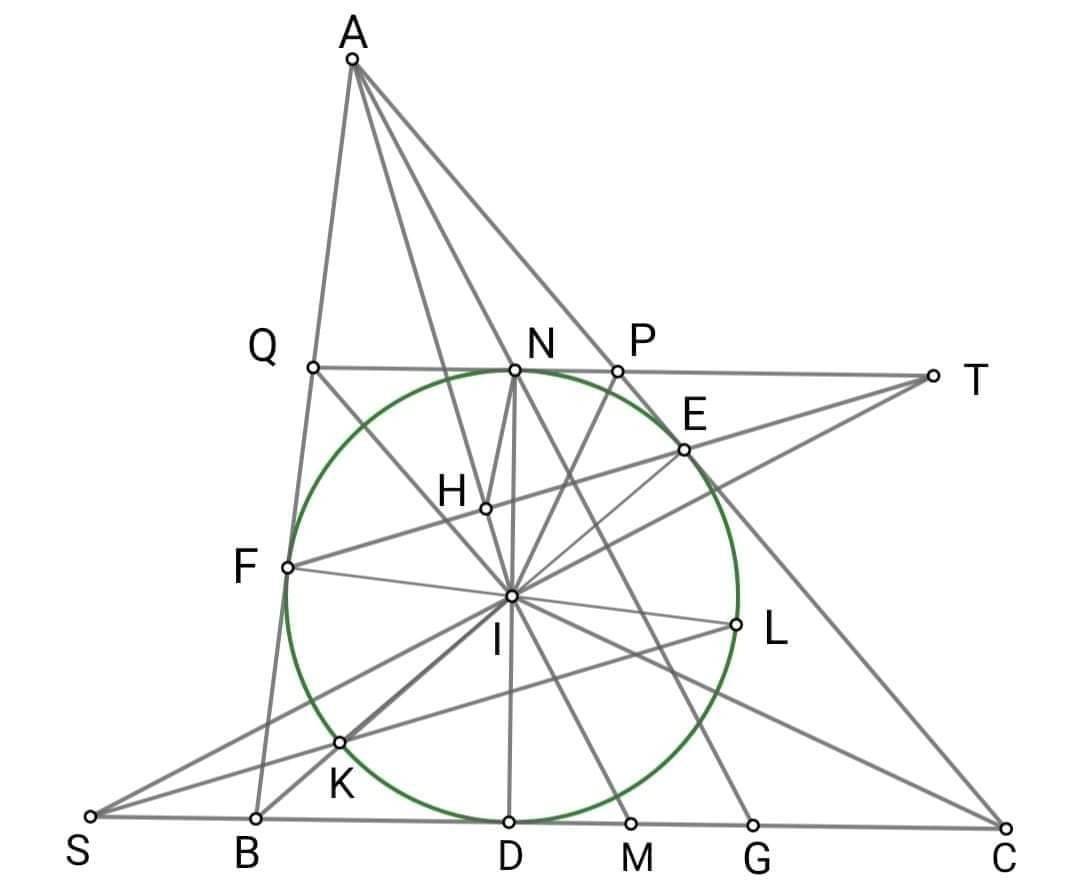

HÌnh bạn tự vẽ.
Bổ đề: (định lý Ptô-lê-mê)
Trong một tứ giác nội tiếp ABCD, ta có:
AC . BD = AB . CD + BC . AD
Áp dụng bổ đề trên cho tứ giác nội tiếp IPAN, ta có IA.NP = IP.AN + IN.AP = 2r(p - a) (ở đây ta đặt BC = a, CA = b, AB = c) và
\(p=\frac{a+b+c}{2}\) thì AN = AP = p - a.
Tương tự IB . PM = 2r(p - b)
IC . MN = 2r(p - c)
Nhân theo vế ba đẳng thức trên ta được:
\(IA.IB.IC.MN.NP.PM=8r^3\left(p-a\right)\left(p-b\right)\left(p-c\right)\).
Mặt khác, vì r là bán kính đường tròn ngoại tiếp \(\Delta MNP\)nên MN.NP.PM = \(4rS_{MNP}\).
Ngoài ra theo công thức Hê-rông ta có:
\(S_{ABC}=\sqrt{p\left(p-a\right)\left(p-b\right)\left(p-c\right)}\).Do đó:
IA . IB . IC. 4rSMNP = \(\frac{8r^3.S^2_{ABC}}{p}=8r^4S_{ABC}\)(vì SABC = pr), suy ra đpcm
P/s: Chỗ nào không hiểu thì bạn chỉ việc vẽ hình ra và quan sát hình là được :))