
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




Bài `13`
\(a,\sqrt{27}+\sqrt{48}-\sqrt{108}-\sqrt{12}\\ =\sqrt{9\cdot3}+\sqrt{16\cdot3}-\sqrt{36\cdot3}-\sqrt{4\cdot3}\\ =3\sqrt{3}+4\sqrt{3}-6\sqrt{3}-2\sqrt{3}\\ =\left(3+4-6-2\right)\sqrt{3}\\ =-\sqrt{3}\\ b,\left(\sqrt{28}+\sqrt{12}-\sqrt{7}\right)\cdot\sqrt{7}+\sqrt{84}\\ =\left(\sqrt{4\cdot7}+\sqrt{4\cdot3}-\sqrt{7}\right)\cdot\sqrt{7}+\sqrt{4\cdot21}\\ =\left(2\sqrt{7}+2\sqrt{3}-\sqrt{7}\right)\cdot\sqrt{7}+2\sqrt{21}\\ =2\cdot7+2\sqrt{21}-7+2\sqrt{21}\\ =14+2\sqrt{21}-7+2\sqrt{21}\\ =7+4\sqrt{21}\)

Rút gọn phương trình đc
\(\left(\sqrt{x+1}+2\right)^2=x+1\)
Xét 2 trường hợp 1 cái là bằng căn của x+1, 1 cái là bằng âm căn của x+1.
rồi giải pt là ra.
Kết luận là X=0

\(A=\sqrt{\left(x+2\right)^2+7}+\sqrt{\left(x-4\right)^2+7}\)
Dạng bài này sử dụng bất đẳng thức Mincopxki \(\sqrt{a^2+b^2}+\sqrt{c^2+d^2}\ge\sqrt{\left(a+c\right)^2+\left(b+d\right)^2}\text{ }\left(1\right)\)
Chứng minh:
\(\left(1\right)\Leftrightarrow a^2+b^2+c^2+d^2+2\sqrt{a^2+b^2}.\sqrt{c^2+d^2}\ge\left(a+c\right)^2+\left(b+d\right)^2\)
\(\Leftrightarrow\sqrt{\left(a^2+b^2\right)\left(c^2+d^2\right)}\ge ac+bd\)
\(+\text{Nếu }ac+bd< 0\text{ thì }VT\ge0>VP,\text{ bđt luôn đúng.}\)
\(\text{+Nếu }ac+bd>0\)
\(\text{bđt}\Leftrightarrow\left(a^2+b^2\right)\left(c^2+d^2\right)\ge\left(ac+bd\right)^2\)
\(\Leftrightarrow\left(ad-bc\right)^2\ge0\)
Do bđt cuối đúng nên bất đẳng thức đã cho cũng đúng.
Vậy ta có đpcm.
Dấu bằng xảy ra khi \(ad=bc\)
\(A=\sqrt{\left(x+2\right)^2+\left(\sqrt{7}\right)^2}+\sqrt{\left(4-x\right)^2+\left(\sqrt{7}\right)^2}\)
\(\ge\sqrt{\left(x+2+4-x\right)^2+\left(\sqrt{7}+\sqrt{7}\right)^2}\)
\(=\sqrt{64}=8.\)
Dấu bằng xảy ra khi \(\left(x+2\right).\sqrt{7}=\left(4-x\right).\sqrt{7}\Leftrightarrow x+2=4-x\Leftrightarrow x=1.\)
Vậy GTNN của biểu thức là 8.

Ta sẽ chứng minh bằng biến đổi tương đương như sau :
Ta có : \(\sqrt{a+b}< \sqrt{a}+\sqrt{b}\left(1\right)\Leftrightarrow\left(\sqrt{a+b}\right)^2< \left(\sqrt{a}+\sqrt{b}\right)^2\Leftrightarrow a+b< a+b+2\sqrt{ab}\)
\(\Leftrightarrow2\sqrt{ab}>0\Leftrightarrow\sqrt{ab}>0\) (luôn đúng)
Vì bất đẳng thức cuối luôn đúng nên bất đẳng thức (1) được chứng minh.
x3 + 3x2 - 25x + 21 = 0
Dạng giải phương trình, mấy thánh giỏi rõ giùm em, đừng ghi tắt nha... Hậu tạ

Cái này nhẩm nghiệm được mà,do tổng các hệ số =0 >>>Pt có 1 nghiệm là 1>>>có chứa nhân tử x-1.
Phân tích:x^3+3x^2-25x+21=x^3-x^2+4x^2-4x-21x+21
=(x^2+4x-21)(x-1)=(x+7)(x-3)(x-1)>>>phương trình có 3 nghiệm là -7,3,1
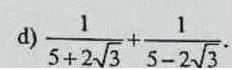 ghi rõ cách làm giùm em ạ
ghi rõ cách làm giùm em ạ
\(\dfrac{1}{5+2\sqrt{3}}+\dfrac{1}{5-2\sqrt{3}}\)
\(=\dfrac{5-2\sqrt{3}+5+2\sqrt{3}}{\left(5-2\sqrt{3}\right)\left(5+2\sqrt{3}\right)}\)
\(=\dfrac{10}{25-12}=\dfrac{10}{13}\)
\(\dfrac{1}{5+2\sqrt{3}}+\dfrac{1}{5-2\sqrt{3}}\\ =\dfrac{5-2\sqrt{3}}{\left(5+2\sqrt{3}\right)\left(5-2\sqrt{3}\right)}+\dfrac{5+2\sqrt{3}}{\left(5+2\sqrt{3}\right)\left(5-2\sqrt{3}\right)}\\ =\dfrac{5-2\sqrt{3}+5+2\sqrt{3}}{\left(5+2\sqrt{3}\right)\left(5-2\sqrt{3}\right)}\\ =\dfrac{10}{5^2-\left(2\sqrt{3}\right)^2}\\ =\dfrac{5+5}{25-12}=\dfrac{10}{13}\)