
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


để em viết ra vậy ạ
cho tam giac mnp vuông tại m (mn>mp) có đường cao mk
a) biết mn=20cm, mp=15cm, tính mk và góc mnp (góc làm tròn đến đơn vị phút).
b) vẽ trung tuyến me của tam giác mnp. từ p vẽ đường thẳng vuông góc với me cắt mn tại d. cm tam giác mnp đồng dạng với tam giác mpd, từ đó suy ra mn.md=np.pk


a.
d đi qua A nên:
\(1\left(m+1\right)-2m+3=2\)
\(\Rightarrow m=2\)
b.
Em tự vẽ
c.
Giả sử điểm cố định mà d luôn đi qua là \(M\left(x_0;y_0\right)\), khi đó với mọi m ta luôn có:
\(y_0=\left(m+1\right)x_0-2m+3\)
\(\Leftrightarrow m\left(x_0-2\right)+x_0-y_0+3=0\)
\(\Rightarrow\left\{{}\begin{matrix}x_0-2=0\\x_0-y_0+3=0\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x_0=2\\y_0=5\end{matrix}\right.\) \(\Rightarrow M\left(2;5\right)\)
d.
- Với \(m=-1\Rightarrow\) d không cắt y=2
- Với \(m\ne-1\)
\(\Rightarrow\left(m+1\right)x-2m+3=2\)
\(\Rightarrow\left(m+1\right)x=2m-1\)
\(\Rightarrow x=\dfrac{2m-1}{m+1}\)
Tọa độ giao điểm của d và y=2 là: \(\left(\dfrac{2m-1}{m+1};2\right)\)

Bài 1:
\(a,\Leftrightarrow m-1\ne0\Leftrightarrow m\ne1\\ b,\Leftrightarrow m-1>0\Leftrightarrow m>1\\ c,\Leftrightarrow m-1< 0\Leftrightarrow m< 1\)
Bài 2:
\(a,\text{Đồng biến}\Leftrightarrow2m>0\Leftrightarrow m>0\\ \text{Nghịch biến}\Leftrightarrow m-1< 0\Leftrightarrow m< 1\\ b,\Leftrightarrow\left\{{}\begin{matrix}2m=m-1\\m+1\ne3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m=-1\\m\ne2\end{matrix}\right.\Leftrightarrow m=-1\)


a: ĐKXĐ: x>=1
\(\sqrt{4x-4}+\sqrt{9x-9}=25\)
=>\(2\sqrt{x-1}+3\sqrt{x-1}=25\)
=>\(5\sqrt{x-1}=25\)
=>x-1=25
=>x=26(nhận)
b: \(\sqrt{4x^2-4x+1}=x-2\)
=>\(\sqrt{\left(2x-1\right)^2}=x-2\)
=>\(\left\{{}\begin{matrix}x>=2\\\left(2x-1\right)^2=\left(x-2\right)^2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x>=2\\\left(2x-1-x+2\right)\left(2x-1+x-2\right)=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x>=2\\\left(x+1\right)\left(3x-3\right)=0\end{matrix}\right.\Leftrightarrow x\in\varnothing\)
c: \(\sqrt{x^2+4x+4}=2x-3\)
=>\(\sqrt{\left(x+2\right)^2}=2x-3\)
=>\(\left\{{}\begin{matrix}x>=\dfrac{3}{2}\\\left(2x-3\right)^2=\left(x+2\right)^2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x>=\dfrac{3}{2}\\\left(2x-3-x-2\right)\left(2x-3+x+2\right)=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x>=\dfrac{3}{2}\\\left(x-5\right)\left(3x-1\right)=0\end{matrix}\right.\Leftrightarrow x=5\)
d: ĐKXĐ: 8-x>=0
=>x<=8
\(\sqrt{8-x}=x-2\)
=>\(\left\{{}\begin{matrix}x-2>=0\\\left(x-2\right)^2=8-x\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2< =x< =8\\x^2-4x+4+x-8=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2< =x< =8\\x^2-3x-4=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2< =x< =8\\\left(x-4\right)\left(x+1\right)=0\end{matrix}\right.\)
=>x=4
e: ĐKXĐ: x>=3
\(\sqrt{x-3}>2\)
=>x-3>4
=>x>7
f: ĐKXĐ: x>=0
\(\dfrac{4}{\sqrt{x}+1}>1\)
=>\(\dfrac{4}{\sqrt{x}+1}-1>0\)
=>\(\dfrac{4-\sqrt{x}-1}{\sqrt{x}+1}>0\)
=>\(3-\sqrt{x}>0\)
=>\(\sqrt{x}< 3\)
=>0<=x<9

b: Vì (d)//(d') nên a=3
Vậy: (d):y=3x+b
Thay x=4 và y=-5 vào (d), ta được:
b+12=-5
hay b=-17




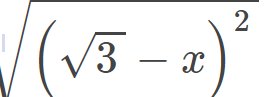
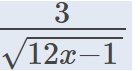 GIÚP MÌNH VỚI Ạ MÌNH CẦN GẤP Ạ
GIÚP MÌNH VỚI Ạ MÌNH CẦN GẤP Ạ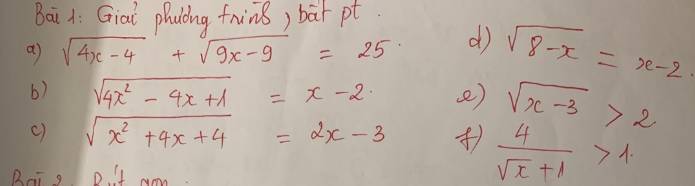
 giúp em với ạ, cần gấp ạ TvT
giúp em với ạ, cần gấp ạ TvT

a: Xét (O) có
AB là tiếp tuyến
AC là tiếp tuyến
Do đó: AB=AC
hay A nằm trên đường trung trực của BC(1)
Ta có: OB=OC
nên O nằm trên đường trung trực của BC(2)
Từ (1) và (2) suy ra AO là đường trung trực của BC