K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
10 tháng 3 2022
\(f\left(x\right)=\dfrac{11x+3}{-x^2+5x-7}.\)
Ta có: \(-x^2+5x-7\) là 1 tam thức bậc 2.
\(\left\{{}\begin{matrix}a=-1< 0.\\\Delta=5^2-4.\left(-1\right).\left(-7\right)=-3< 0.\end{matrix}\right.\)
\(\Rightarrow-x^2+5x-7>0\forall x\in R.\)
\(\Rightarrow\) \(f\left(x\right)>0.\Leftrightarrow11x+3>0.\Leftrightarrow x>\dfrac{-3}{11}.\\ f\left(x\right)< 0.\Leftrightarrow11x+3>0.\Leftrightarrow x>\dfrac{-3}{11}.\\ f\left(x\right)=0.\Leftrightarrow x=\dfrac{-3}{11}.\)
NV
Nguyễn Việt Lâm
Giáo viên
14 tháng 3 2020
1.
\(f\left(x\right)=\frac{x-7}{\left(x-4\right)\left(4x-3\right)}\)
Vậy:
\(f\left(x\right)\) ko xác định tại \(x=\left\{\frac{3}{4};4\right\}\)
\(f\left(x\right)=0\Rightarrow x=7\)
\(f\left(x\right)>0\Rightarrow\left[{}\begin{matrix}\frac{3}{4}< x< 4\\x>7\end{matrix}\right.\)
\(f\left(x\right)< 0\Rightarrow\left[{}\begin{matrix}x< \frac{3}{4}\\4< x< 7\end{matrix}\right.\)
2.
\(f\left(x\right)=\frac{11x+3}{-\left(x-\frac{5}{2}\right)^2-\frac{3}{4}}\)
Vậy:
\(f\left(x\right)=0\Rightarrow x=-\frac{3}{11}\)
\(f\left(x\right)>0\Rightarrow x< -\frac{3}{11}\)
\(f\left(x\right)< 0\Rightarrow x>-\frac{3}{11}\)
NV
Nguyễn Việt Lâm
Giáo viên
14 tháng 3 2020
3.
\(f\left(x\right)=\frac{3x-2}{\left(x-1\right)\left(x^2-2x-2\right)}\)
Vậy:
\(f\left(x\right)\) ko xác định khi \(x=\left\{1;1\pm\sqrt{3}\right\}\)
\(f\left(x\right)=0\Rightarrow x=\frac{2}{3}\)
\(f\left(x\right)>0\Rightarrow\left[{}\begin{matrix}x< 1-\sqrt{3}\\\frac{2}{3}< x< 1\\x>1+\sqrt{3}\end{matrix}\right.\)
\(f\left(x\right)< 0\Rightarrow\left[{}\begin{matrix}1-\sqrt{3}< x< \frac{2}{3}\\1< x< 1+\sqrt{3}\end{matrix}\right.\)
4.
\(f\left(x\right)=\frac{\left(x-2\right)\left(x+6\right)}{\sqrt{6}\left(x+\frac{\sqrt{6}}{4}\right)^2+\frac{8\sqrt{2}-3\sqrt{6}}{8}}\)
Vậy:
\(f\left(x\right)=0\Rightarrow x=\left\{-6;2\right\}\)
\(f\left(x\right)>0\Rightarrow\left[{}\begin{matrix}x< -6\\x>2\end{matrix}\right.\)
\(f\left(x\right)< 0\Rightarrow-6< x< 2\)
HT
1
NV
Nguyễn Việt Lâm
Giáo viên
26 tháng 3 2022
\(f\left(x\right)=\dfrac{\left(3x-4\right)\left(2x-3\right)}{\left(x^2-5x+6\right)\left(5-x\right)}>0\)
\(\Leftrightarrow\dfrac{\left(3x-4\right)\left(2x-3\right)}{\left(x-2\right)\left(x-3\right)\left(5-x\right)}>0\)
Bảng xét dấu:
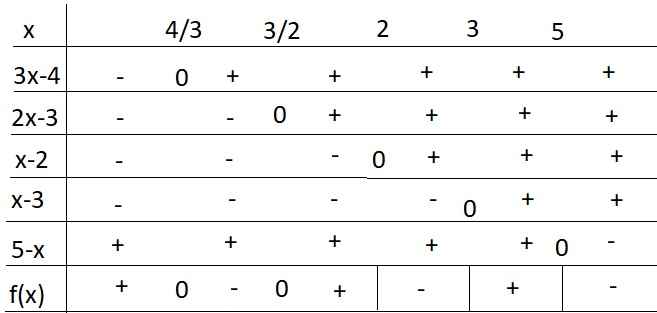
Từ bảng xét dấu ta thấy nghiệm của BPT là: \(\left[{}\begin{matrix}x< 5\\\dfrac{3}{2}< x< 2\\3< x< 5\end{matrix}\right.\)
13 tháng 2 2017
c/m:
\(f\left(x_1\right)-f\left(x_2\right)=5x_1-5x_2=5\left(x_1-x_2\right)< 0\) do x1<x2
Vậy ;\(f\left(x_1\right)-f\left(x_2\right)< 0\Rightarrow f\left(x_1\right)< f\left(x_2\right)\Rightarrow\)Điều phải chứng minh ngược lại.
22 tháng 9 2021
a: \(A=\left\{0;1;2;3;4;5\right\}\)
b: \(B=\left\{2;3;4;5\right\}\)
c: \(C=\left\{0;1;-1;2;-2;3;-3\right\}\)
PT
1
CM
7 tháng 4 2017
f(x) = x2 – 5x +4
f(4)= 0; f(2) = -2 < 0; f(-1)= 10 > 0; f(0) = 4 > 0