K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
O
27 tháng 3 2022
f) \(\dfrac{-x}{3}=2\dfrac{1}{7}\div\dfrac{5}{7}\)
\(\dfrac{-x}{3}=\dfrac{15}{7}\div\dfrac{5}{7}\)
\(\dfrac{-x}{3}=3\)
\(-x=3\cdot3\)
\(-x=9\)
\(x=-9\)
g) \(\dfrac{5}{4}+\dfrac{1}{4}\div x=1\dfrac{3}{8}\)
\(\dfrac{5}{4}+\dfrac{1}{4}\div x=\dfrac{11}{8}\)
\(\dfrac{1}{4}\div x=\dfrac{11}{8}-\dfrac{5}{4}\)
\(\dfrac{1}{4}\div x=\dfrac{1}{8}\)
\(x=\dfrac{1}{4}\div\dfrac{1}{8}\)
\(x=2\)
29 tháng 12 2022
TK :
5x + 5x +2 = 650
5x + 5x . 52 = 650
5x .( 1 +25 ) = 650
5x .26 = 650
5x = 650 / 26 =25
5x = 52
nên x=2
R
5 tháng 5 2023
\(\dfrac{-7}{x+1}=\dfrac{6}{x+27}\)
\(\Rightarrow-7x-189=6x+6\)
\(\Rightarrow-7x-6x=6+189\)
\(\Rightarrow-13x=195\)
\(\Rightarrow x=-15\)
Vay x = -15
DG
1
AH
Akai Haruma
Giáo viên
31 tháng 10 2023
Lời giải:
Gọi $d=ƯCLN(3n+2, 2n+3)$
$\Rightarrow 3n+2\vdots d; 2n+3\vdots d$
$\Rightarrow 3(2n+3)-2(3n+2)\vdots d$
$\Rightarrow 5\vdots d$
$\Rightarrow d=1$ hoặc $d=5$.
Để ps đã cho là tối giản thì $d\neq 5$. Nghĩa là $2n+3\not\vdots 5$
$\Rightarrow 2n-2\not\vdots 5$
$\Rightarrow 2(n-1)\not\vdots 5$
$\Rightarrow n-1\not\vdots 5$
$\Rightarrow n\neq 5k+1$ với $k$ tự nhiên.
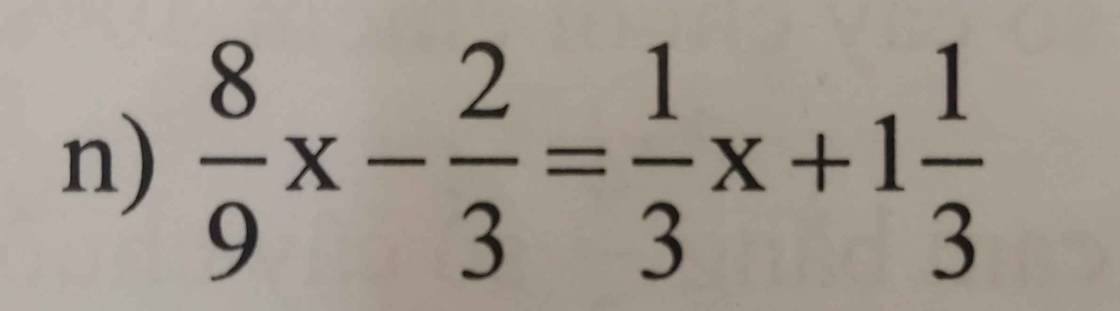
\(\dfrac{8}{9}x-\dfrac{2}{3}=\dfrac{1}{3}x+1\dfrac{1}{3}\)
=>\(\dfrac{8}{9}x-\dfrac{1}{3}x=1+\dfrac{1}{3}+\dfrac{2}{3}\)
=>\(\dfrac{5}{9}x=2\)
=>\(x=2:\dfrac{5}{9}=2\cdot\dfrac{9}{5}=\dfrac{18}{5}\)