K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
HQ
Hà Quang Minh
Giáo viên
30 tháng 9 2023
Giả sử bác Việt chèo thuyền cập bến ở vị trí M và ta đặt BM=x (km) (x>0)
Ta có: MC=BC-BM=9,25-x (km)
Thời gian di chuyển của anh Nam đến điểm hẹn gặp nhau là \(\frac{{9,25 - x}}{5}\)\(\)(giờ)
Tam giác ABM vuông tại B, nên ta có:
\(\)\(A{M^2} = A{B^2} + B{M^2} = {x^2} + 16\)
=> \(AM = \sqrt {{x^2} + 16} \) (km)
Thời gian di chuyển của bác Việt đến điểm hẹn găp nhau là: \(\frac{{\sqrt {{x^2} + 16} }}{4}\) (giờ)
Để hai người không phải chờ nhau thì ta có phương trình:
\(\frac{{\sqrt {{x^2} + 16} }}{4} = \frac{{9,25 - x}}{5}\)\( \Leftrightarrow 5\sqrt {{x^2} + 16} = 37 - 4x\)
Bình phương hai vế của phương trình trên ta được:
\(25({x^2} + 16) = 16{x^2} - 296x + 1369\)
\( \Leftrightarrow 9{x^2} + 296x - 969 = 0\)
\( \Leftrightarrow x = 3\) hoặc \(x = - \frac{{323}}{9}\)
Thử lại ta thấy cả hai giá trị của x đều thỏa mãn
Mà x>0 nên ta chọn x=3
Vậy vị trí hai người gặp nhau cách bến Bính 3km và cách thôn Hoành 6,25 km.
TA
2 tháng 8 2021
Điểm đầu là A: `\vec(AB), \vec(AC),\vec(AD),\vec(AE)`
Điểm đầu là B: `\vec(BA),\vec(BC),\vec(BD),\vec(BE)`.
4 tháng 8 2016
Lúc đầu bố A có 50 ngàn đ, mẹ A có 50 ngàn đ, A có 0 ngàn đ
Sau cùng :
Bố A có 1 ngàn + số tiền 49 ngàn mà A nợ (sẽ trả) ---> Bố A vẫn " có " 50 ngàn đ
Mẹ A có 1 ngàn + số tiền 49 ngàn mà A nợ (sẽ trả) ---> Mẹ A vẫn " có " 50 ngàn đ
A có 1 ngàn + 1 cái áo (trị giá 97 ngàn) + món nợ 98 ngàn ---> A có 1+97-98 = 0 (ngàn đ)
Như vậy Mon và Xê lúc đầu mỗi người có 50 ngàn thì sau cùng mỗi người vẫn "có" 50 ngàn
Nô lúc đầu có 0 ngàn đ thì sau cùng vẫn " có 0 ngàn đ "
Không có ai mất tiền cả !
Không phải tính theo kiểu 49 x 2+1 rồi bảo thiếu 1 ngàn ( 49 x 2 là tiền "nợ", 1 là tiền "có", không thể cộng vào nhau được )
Mà phải tính là 1 + 97 - 49 x 2 = 0
4 tháng 8 2016
Lúc đầu Mon có 50 ngàn đ, Xê có 50 ngàn đ, Nô có 0 ngàn đ
Sau cùng :
Mon có 1 ngàn + số tiền 49 ngàn mà Nô nợ (sẽ trả) ---> Mon vẫn " có " 50 ngàn đ
Xê có 1 ngàn + số tiền 49 ngàn mà Nô nợ (sẽ trả) ---> Xê vẫn " có " 50 ngàn đ
Nô có 1 ngàn + 1 cái áo (trị giá 97 ngàn) + món nợ 98 ngàn ---> Nô có 1+97-98 = 0 (ngàn đ)
Như vậy Mon và Xê lúc đầu mỗi người có 50 ngàn thì sau cùng mỗi người vẫn "có" 50 ngàn
Nô lúc đầu có 0 ngàn đ thì sau cùng vẫn " có 0 ngàn đ "
Không có ai mất tiền cả !
Không phải tính theo kiểu 49x2+1 rồi bảo thiếu 1 ngàn (49x2 là tiền "nợ", 1 là tiền "có", không thể cộng vào nhau được !)
Mà phải tính là 1 + 97 - 49 x 2 = 0
BD
12 tháng 8 2016
\(2\frac{4}{5}x-50:\frac{2}{3}=51\)
\(\frac{14}{5}x-50:\frac{2}{3}=51\)
\(\frac{14}{51}x=51+50:\frac{2}{3}\)
\(\frac{14}{51}x=51+75\)
\(\frac{14}{51}x=126\)
\(x=126:\frac{14}{51}\)
\(x=459\)
CM
27 tháng 6 2017
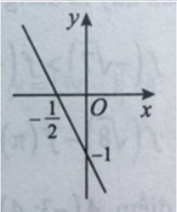
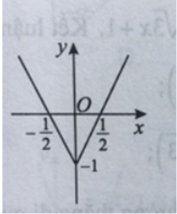
Ta có y = 2 x - 1 = 2 x - 1 ; x ≥ 0 - 2 x - 1 ; x < 0 .
Đường thẳng y = 2x – 1 đi qua điểm (0 ; -1) và 1 2 ; 0
Đường thẳng y = -2x – 1 đi qua điểm (0; -1) và - 1 2 ; 0
Vì vậy đồ thị hàm số y = 2 x - 1 là hình theo phương án C.
Nhận xét: Học sinh có thể nhầm khi cho y = 2 x - 1 = 2 x - 1 (phương án A) hoặc y = 2 x - 1 = - 2 x - 1 (phương án B), hoặc chọn nhầm các nhánh (phương án D).
nước
vừa ở nc vừa ở cạn