K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
BV
1
AH
Akai Haruma
Giáo viên
20 tháng 11 2021
Lời giải:
Đặt $xy=k$. Ta có:
$x_1y_1=k=x_2y_2$
Thay $x_1=6; x_2=-9\Rightarrow 6y_1=-9y_2$
$\Leftrightarrow y_1=-1,5y_2$
$y_1-y_2=10$
$-1,5y_2-y_2=10$
$-2,5y_2=10$
$y_2=-4$
$y_1=-1,5y_2=-1,5.(-4)=6$
27 tháng 10 2021
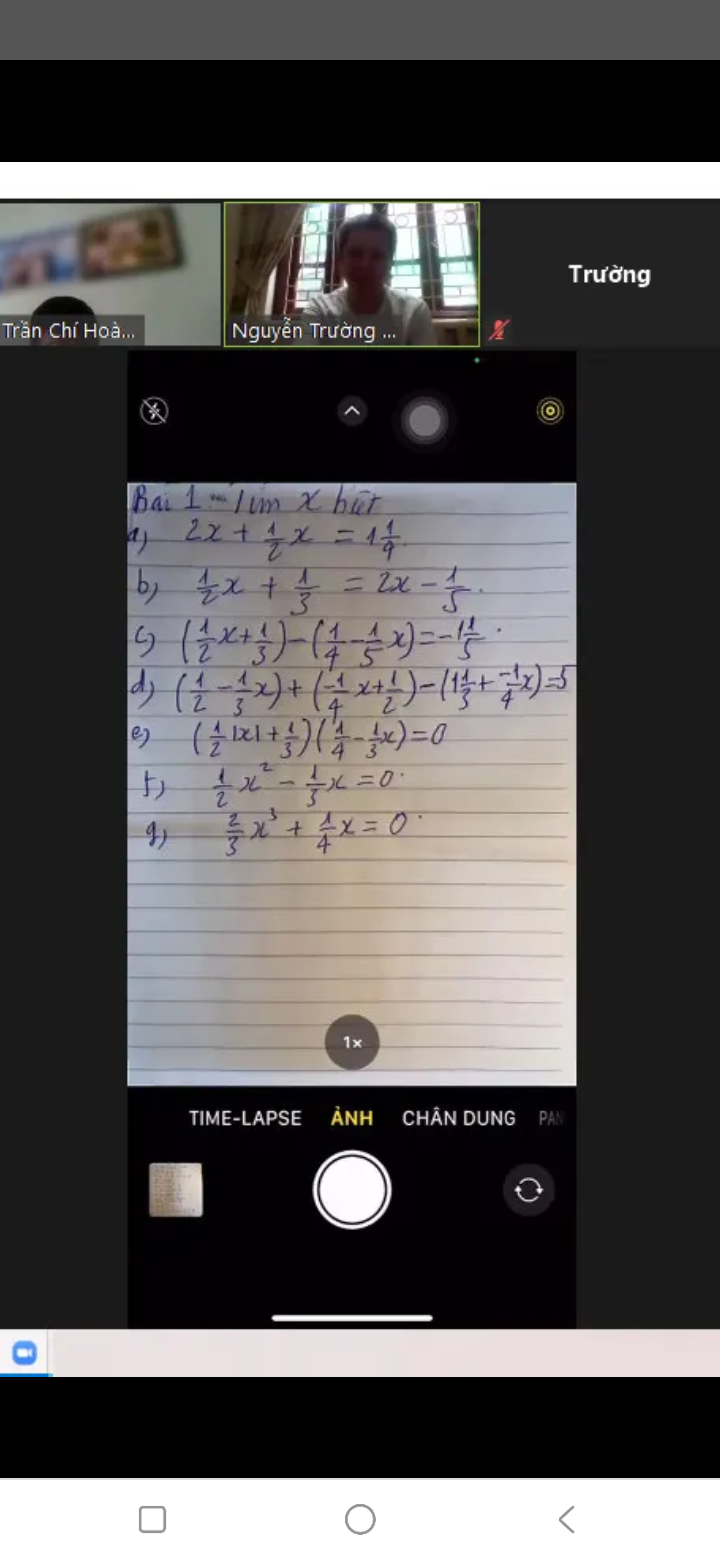
a) (1,75 : \(\dfrac{7}{2}\)).\(\dfrac{8}{5}\)=(\(\dfrac{7}{4}\) : \(\dfrac{7}{2}\)).\(\dfrac{8}{5}\)=(\(\dfrac{7}{4}\).\(\dfrac{2}{7}\)).\(\dfrac{8}{5}\)=\(\dfrac{1}{2}\).\(\dfrac{8}{5}\)=\(\dfrac{4}{5}\)
b) \(\dfrac{7}{2}\).\(4\dfrac{5}{3}\)-\(2\dfrac{5}{3}\).\(\dfrac{7}{2}\)=(\(4\dfrac{5}{3}\)-\(2\dfrac{5}{3}\)).\(\dfrac{7}{2}\)=2.\(\dfrac{7}{2}\)=7
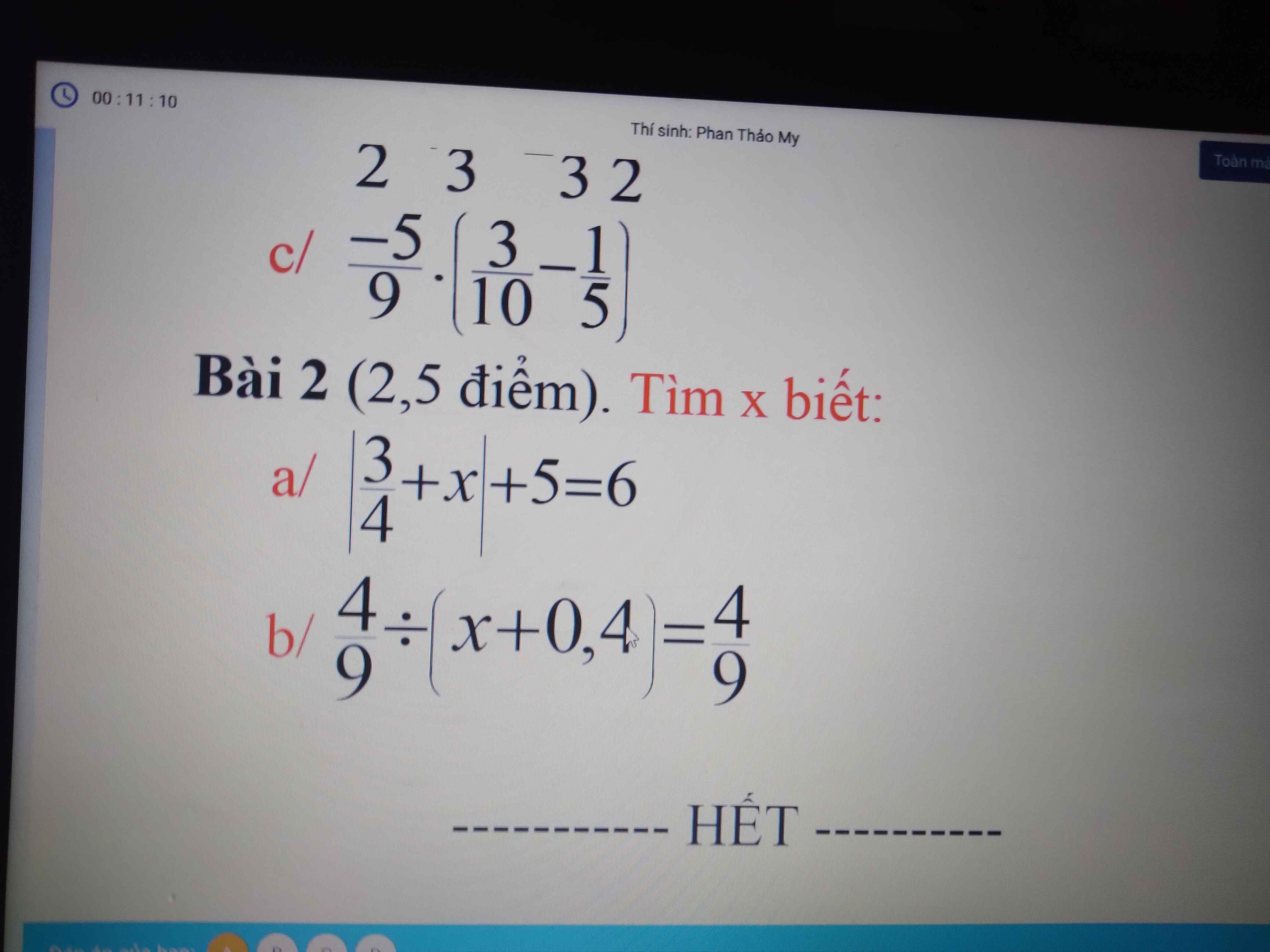
c)\(\dfrac{-5}{9}\).(\(\dfrac{3}{10}-\dfrac{1}{5}\))=\(\dfrac{-5}{9}\).(\(\dfrac{3}{10}-\dfrac{2}{10}\))=\(\dfrac{-5}{9}\).\(\dfrac{1}{10}\)=\(\dfrac{-1}{18}\)
27 tháng 10 2021
Bài 2:
\(a,\Rightarrow\left|\dfrac{3}{4}+x\right|=1\Leftrightarrow\left[{}\begin{matrix}\dfrac{3}{4}+x=1\\\dfrac{3}{4}+x=-1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{1}{4}\\x=-\dfrac{7}{4}\end{matrix}\right.\\ b,\Leftrightarrow x+\dfrac{2}{5}=\dfrac{4}{9}:\dfrac{4}{9}=1\Leftrightarrow x=\dfrac{3}{5}\)
27 tháng 10 2021
b: \(\dfrac{4}{9}:\left(x+\dfrac{2}{5}\right)=\dfrac{4}{9}\)
\(\Leftrightarrow x+\dfrac{2}{5}=1\)
hay \(x=\dfrac{3}{5}\)
19 tháng 2 2023
x và y tỉ lệ thuận
nên \(\dfrac{x_1}{y_1}=\dfrac{x_2}{y_2}\)
Áp dụng tính chất của DTSBN, ta được:
\(\dfrac{x_1}{y_1}=\dfrac{x_2}{y_2}=\dfrac{2x_1-3x_2}{2y_1-3y_2}=\dfrac{42.5}{-8.5}=-5\)
=>x=-5y
LT
* Mọi người cố giúp em hoàn thiện trong buổi tối nay với ạ, em đg cần gấp! Cảm ơn ạ!
1
25 tháng 3 2023
12:
a: Xét ΔABM và ΔACM có
AB=AC
BM=CM
AM chung
=>ΔABM=ΔACM
=>góc BAM=góc CAM
=>AM là phân giác của góc BAC
b: Xét ΔNAC và ΔNBE có
góc NAC=góc NBE
NA=NB
góc ANC=góc BNE
=>ΔNAC=ΔNBE
=>AC=BE
c: Xét tứ giác AEBC có
AC//BE
AC=BE
=>AEBC là hình bình hành
=>AE//BC
d: Xét ΔEAC có EF/EA=EN/EC
nên FN//AC//EB
Xét ΔECB có CM/CB=CN/CE
nên NM//EB
=>F,N,M thẳng hàng
C
4 tháng 5 2022
Áp dung định lí Pytago ta có
AB2 + AC2 = BC2
hay 32 + AC2 = 52
AC2 = 52-32
AC2 = 252-92
AC2 = \(\sqrt{16}\)
AC= 4cm
4 tháng 5 2022
Áp dung định lí Pytago ta có
AB2 + AC2 = BC2
hay 32 + AC2 = 52
AC2 = 52-32
AC2 = 25-9
AC = √16
AC= 4cm
Với \(x+y+z+t=0\Leftrightarrow x+y+z=-t\)
\(\Leftrightarrow M=\dfrac{-t}{t}=-1\\ \Leftrightarrow\left(M-1\right)^{2020}=0\)
Với \(x+y+z+t\ne0\)
\(\Leftrightarrow M=\dfrac{3\left(x+y+z+t\right)}{x+y+z+t}=3\left(\text{tc dtsbn}\right)\\ \Leftrightarrow\left(M-1\right)^{2020}=\left(3-1\right)^{2020}=2^{2020}\)