Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) x + \(\sqrt{\left(x-2^{ }\right)^2}\)= x +\(|x-2|\)= x +2-x (vì x<2)
b) \(\sqrt{\left(x-3\right)^2}\)-x = \(|x-3|-x=x-3-x\) (vì x>3)
c) m- \(\sqrt{m^2-2m+1}=m-\sqrt{\left(m-1\right)^2}\)
Những con còn lại bạn làm như trên và rút gọn đi là được
d: \(=x+y-\left|x-y\right|\)
=x+y-x+y=2y
e: \(=\left|5a-1\right|-4a=\left|5\cdot\dfrac{1}{2}-1\right|-2\)
\(=\dfrac{5}{2}-1-2=\dfrac{5}{2}-3=-\dfrac{1}{2}\)
f: \(=\left|2a-3\right|-4a-1\)
\(=\left|-10-3\right|-4\cdot\left(-5\right)-1=13+20-1=32\)

a/ \(\sqrt{4a^4-12a^2+9}-\sqrt{a^4-8a^2+16}\)
= \(\sqrt{\left(2a^2-3\right)^2}-\sqrt{\left(a^2-4\right)^2}\)
= \(|2a^2-3|-|a^2-4|\)
= \(2a^2-3+a^2-4\)
= \(3a^2-7\)
Thay a=\(\sqrt{3}\).Ta có:
\(3.\left(\sqrt{3}\right)^2-7\)
= 3.3-7=2
b/ \(\sqrt{10a^2-12a\sqrt{10}+36}\)
= \(\sqrt{\left(a\sqrt{10}\right)^2-2.a\sqrt{10}.6+6^2}\)
= \(\sqrt{\left(a\sqrt{10}-6\right)^2}\)
= \(|a\sqrt{10}-6|\)
= \(-a\sqrt{10}+6\)
Thay a= \(\sqrt{\frac{5}{2}}-\sqrt{\frac{2}{5}}\)=\(\frac{3}{\sqrt{10}}\),Ta có:
\(-\frac{3}{\sqrt{10}}.\sqrt{10}+6\)
= -3+6 =3

A=|m+1|+|m-1|=|m+1|+|1-m|>=|m+1+1-m|=2
Dấu = xảy ra khi -1<=m<=1
B=|2a-1|+|2a-3|=|2a-1|+|3-2a|>=|2a-1+3-2a|=2
Dấu = xảy ra khi 1/2<=a<=3/2

a) \(\sqrt{-9a}-\sqrt{9+12a+4a^2}\) \(=\sqrt{9.\left(-a\right)}-\sqrt{\left(3+2a\right)^2}=3\sqrt{-a}-\left|3+2a\right|\)
\(=3\sqrt{9}-\left|3+2\left(-9\right)\right|=3.3-15=-6\)
b) \(1+\dfrac{3m}{m-2}\sqrt{m^2-4x+4}=1+\dfrac{3m}{m-2}\sqrt{\left(m-2\right)^2}=1+\dfrac{3m\left|m-2\right|}{m-2}\)
\(=\left\{{}\begin{matrix}1+3m\left(nếu\left(m-2\right)>0\right)\\1-3m\left(nến\left(m-2\right)< 0\right)\end{matrix}\right.\) \(=\left\{{}\begin{matrix}1+3m\left(nếu\left(m>2\right)\right)\\1-3m\left(nếu\left(m< 2\right)\right)\end{matrix}\right.\)
ta có : \(m=1,5< 2\) vậy giá trị của biểu thức tại m = 1,5 là \(1-3m\) = \(1-3.1,5=-3,5\)
c) \(\sqrt{1-10a+25a^2}-4a=\sqrt{\left(1-5a\right)^2}-4a=\left|1-5a\right|-4a\)
\(=\left\{{}\begin{matrix}1-9a\left(nếu\left(1-5a\right)\ge0\right)\\a-1\left(nếu\left(1-5a\right)< 0\right)\end{matrix}\right.\) \(=\left\{{}\begin{matrix}1-9a\left(nếu\left(a\le\dfrac{1}{5}\right)\right)\\a-1\left(nếu\left(a>\dfrac{1}{5}\right)\right)\end{matrix}\right.\)
ta có : \(a=\sqrt{2}>\dfrac{1}{5}\) vậy giá trị của biểu thức tại \(a=\sqrt{2}\) là a - 1 = \(\sqrt{2}-1\)
d) \(4x-\sqrt{9x^2+6x+1}=4x-\sqrt{\left(3x+1\right)^2}=4x-\left|3x+1\right|\)
\(=\left\{{}\begin{matrix}x-1\left(nếu\left(x\ge-\dfrac{1}{3}\right)\right)\\7x+1\left(nếu\left(x< -\dfrac{1}{3}\right)\right)\end{matrix}\right.\)
ta có : \(x=-\sqrt{3}< -\dfrac{1}{3}\) vậy giá trị của biểu thức tại \(x=-\sqrt{3}\) là \(7.\left(-\sqrt{3}\right)+1=1-7\sqrt{3}\)

1.
a) \(A=\sqrt{1}-4a+4a^2-2a\)
\(A=4a^2-6a+1\)
b) \(B=\frac{5-x}{x^2-10x+25}=\frac{-\left(x-5\right)}{\left(x-5\right)^2}=\frac{-1}{x-5}\)
c) \(C=\sqrt{\left(x-1\right)^2}+\frac{x-1}{\sqrt{x^2-2x+1}}\)
\(C=\left|x-1\right|+\frac{x-1}{\sqrt{\left(x-1\right)^2}}=\left|x-1\right|+\frac{x-1}{\left|x-1\right|}\)
+) Xét \(x-1>0\Leftrightarrow x>1\)ta có \(C=x-1+\frac{x-1}{x-1}=x-1+1=x\)
+) Xét \(x-1< 0\Leftrightarrow x< 1\)ta có \(C=1-x+\frac{x-1}{1-x}=1-x-1=-x\)
2.
a) \(\sqrt{2-\sqrt{3}}\cdot\sqrt{2+\sqrt{3}}\)
\(=\sqrt{\left(2-\sqrt{3}\right)\left(2+\sqrt{3}\right)}\)
\(=\sqrt{4-3}=1\)
b) \(\sqrt{3\sqrt{2}-2\sqrt{3}}\cdot\sqrt{3\sqrt{2}+2\sqrt{3}}\)
\(=\sqrt{\left(3\sqrt{2}-2\sqrt{3}\right)\left(3\sqrt{2}+2\sqrt{3}\right)}\)
\(=\sqrt{\left(3\sqrt{2}\right)^2-\left(2\sqrt{3}\right)^2}\)
\(=\sqrt{18-12}=\sqrt{6}\)
c) Sửa luôn đề \(\sqrt{13-4\sqrt{3}}+\sqrt{7+4\sqrt{3}}\)
\(=\sqrt{\left(2\sqrt{3}\right)^2-2\cdot2\sqrt{3}\cdot1+1}+\sqrt{2^2+2\cdot2\cdot\sqrt{3}+3}\)
\(=\sqrt{\left(2\sqrt{3}-1\right)^2}+\sqrt{\left(2+\sqrt{3}\right)^2}\)
\(=\left|2\sqrt{3}-1\right|+\left|2+\sqrt{3}\right|\)
\(=2\sqrt{3}-1+2+\sqrt{3}\)
\(=3\sqrt{3}+1\)

\(a)\sqrt{-9a}-\sqrt{9+12a+4a^2}\)
\(==\sqrt{3^2.\left(-a\right)}-\sqrt{3^2-2.3.2a+\left(2a\right)^2}\)
\(=3\sqrt{-a}-\sqrt{\left(3+2a\right)^2}\)
\(=3\sqrt{a}-\left|3+2a\right|\)
\(b)1+\frac{3m}{m-2}\sqrt{m^2-4m+4}\)
\(=1+\frac{3m}{m-2}\sqrt{\left(m\right)^2-2.2m+2^2}\)
\(=1+\frac{3m}{m-2}\sqrt{\left(m-2\right)^2}\)
\(=1+\frac{3m}{m-2}|m-2|\)
\(c)4x-\sqrt{9x^2+6x+1}\)
\(=4x-\sqrt{\left(3x\right)^2+2.3x+1}\)
\(=4x-\sqrt{\left(3x+1\right)^2}\)
\(=4x-|3x+1|\)

Từ kết quả bài toán suy ngược ra thôi
Muốn giải thích thì cứ phá 2 vế ra rồi so sánh là tìm ra cách tách biểu thức
Câu 4 mình ko biết giải quyết kiểu lớp 9 (mặc dù chắc chắn là biểu thức sẽ được biến đổi như vầy)
Đó là kiểu trình bày của lớp 11 hoặc 12 để bạn tham khảo thôi

Bài 3: Em thử thôi, sai bỏ qua cho ạ.
c)ĐK: \(\left\{{}\begin{matrix}x^2-5x+4\ge0\\x\ge1\end{matrix}\right.\)
\(\left(x-4\right)\left(x-1\right)=2\sqrt{x-1}\)
Đặt \(\sqrt{x-1}=t\ge0\) suy ra:
\(\left(x-4\right)t^2-2t=0\Leftrightarrow t\left(t\left(x-4\right)-2\right)=0\)
+) Với t = 0 thì x = 1
+) \(t\left(x-4\right)=2\). Nhận xét x = 4 không phải là nghiệm.
Xét x khác 4, khi đó \(\sqrt{x-1}=\frac{2}{x-4}\Leftrightarrow..\)
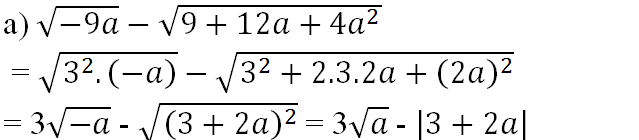
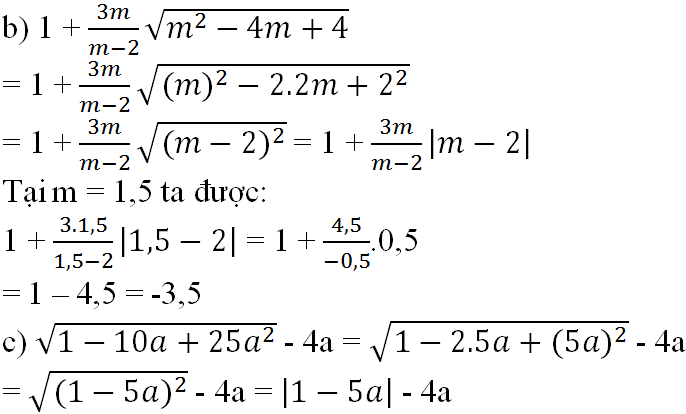
cái phần A là thiếu dấu cộng đấy ạ
Em thử nha!Sai thì thôi:((
\(A=\left|m+1\right|+\left|m-1\right|=\left|m+1\right|+\left|1-m\right|\ge\left|m+1+1-m\right|=2\)
Dấu"=" xảy ra khi \(\left(m+1\right)\left(1-m\right)\ge0\Leftrightarrow-m^2+1\Leftrightarrow-1\le m\le1\)
\(B=\sqrt{\left(2a\right)^2-2.2a.1+1}+\sqrt{4a^2-2.2a.3+9}\)
\(=\left|2a-1\right|+\left|2a-3\right|=\left|2a-1\right|+\left|3-2a\right|\ge2\)
Dấu "=" xảy ra khi...