K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NT
1
29 tháng 7 2021
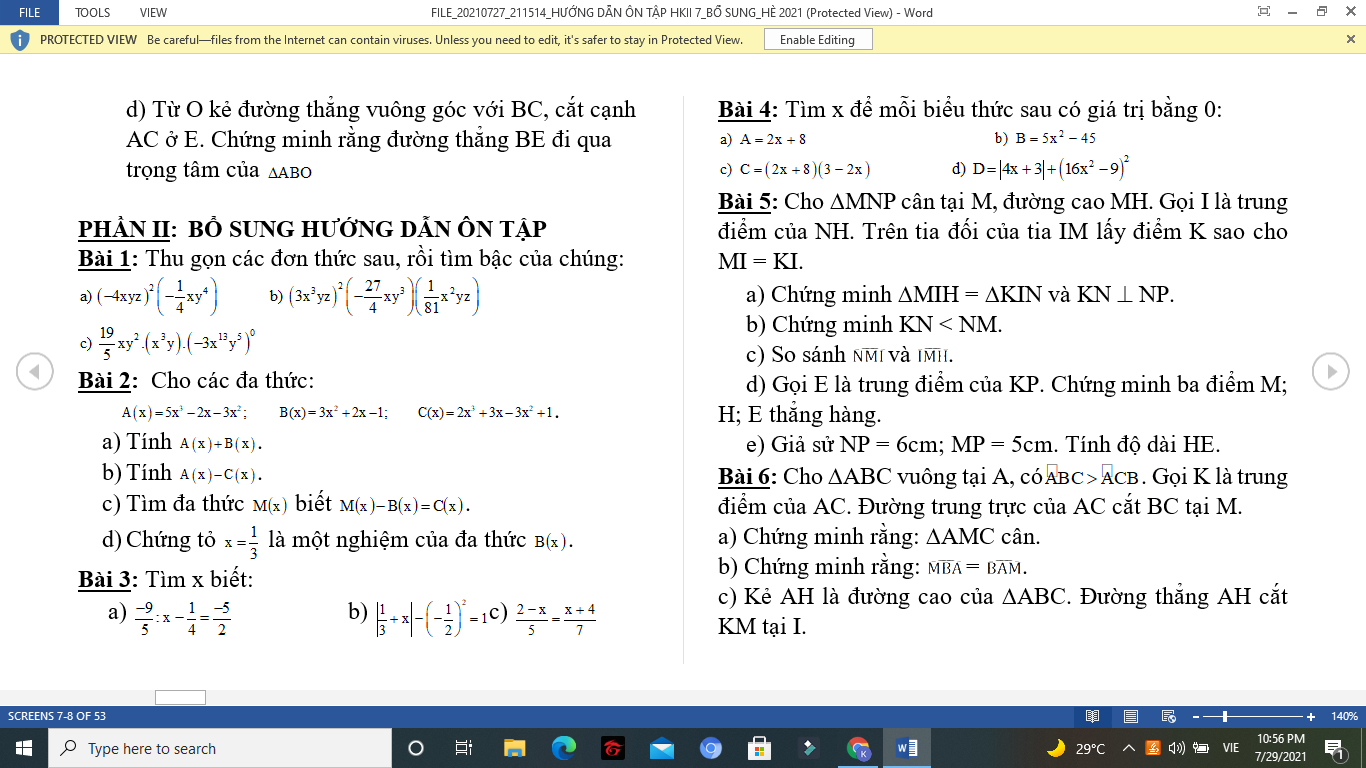
Bài 3:
c) Ta có: \(\dfrac{2-x}{5}=\dfrac{x+4}{7}\)
\(\Leftrightarrow14-7x=5x+20\)
\(\Leftrightarrow-7x-5x=20-14\)
\(\Leftrightarrow-12x=6\)
hay \(x=-\dfrac{1}{2}\)
1 tháng 7 2021
Bài 4:
a) Xét ΔABE và ΔHBE có
BA=BH(gt)
\(\widehat{ABE}=\widehat{HBE}\)(BE là tia phân giác của \(\widehat{ABH}\))
BE chung
Do đó: ΔABE=ΔHBE(c-g-c)
b) Ta có: ΔABE=ΔHBE(cmt)
nên EA=EH(hai cạnh tương ứng)
Ta có: BA=BH(gt)
nên B nằm trên đường trung trực của AH(Tính chất đường trung trực của một đoạn thẳng)(1)
Ta có: EA=EH(cmt)
nên E nằm trên đường trung trực của AH(Tính chất đường trung trực của một đoạn thẳng)(2)
Từ (1) và (2) suy ra BE là đường trung trực của AH
c) Ta có: ΔABE=ΔHBE(cmt)
nên \(\widehat{BAE}=\widehat{BHE}\)(hai góc tương ứng)
mà \(\widehat{BAE}=90^0\)(gt)
nên \(\widehat{BHE}=90^0\)
Xét ΔBKC có
KH là đường cao ứng với cạnh BC
CA là đường cao ứng với cạnh BK
KH cắt CA tại E
Do đó: E là trực tâm của ΔBKC(Tính chất ba đường cao của tam giác)
d) Ta có: EA=EH(cmt)
mà EH<EC(ΔEHC vuông tại H có EC là cạnh huyền)
nên EA<EC
TK
1
17 tháng 10 2021
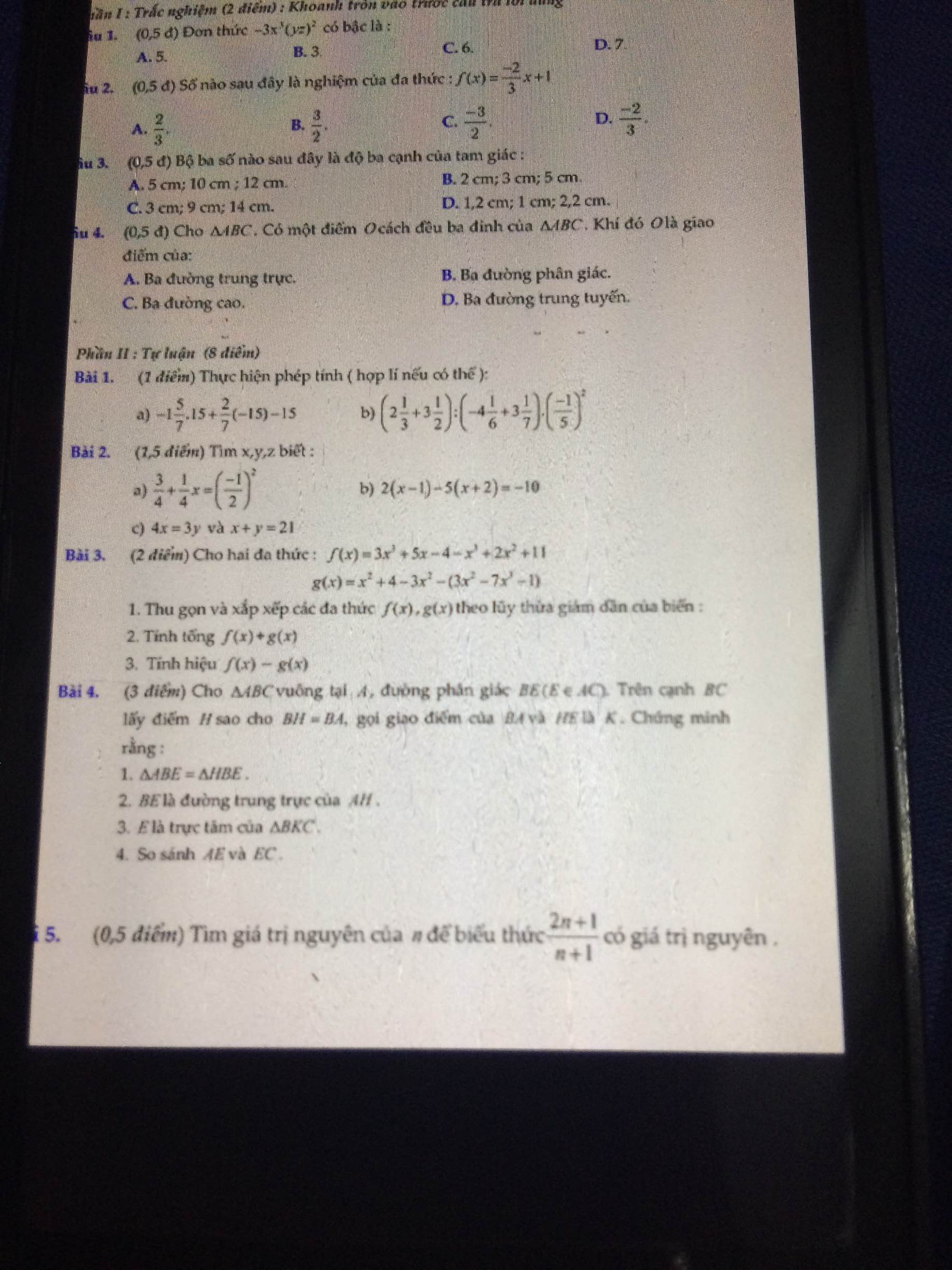
Câu 3:
a: Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{3}=\dfrac{y}{2}=\dfrac{x+y}{3+2}=\dfrac{90}{5}=18\)
Do đó: x=54; y=36
0H
Chỉ cần giải giúp em câu c,d thui ạ
1
24 tháng 5 2022
a: Xét ΔEAB có \(\widehat{EBA}=\widehat{EAB}\)
nên ΔEAB cân tại E
mà EK là đường cao
nen K là trung điểm của AB
hay KA=KB
b: Xét ΔACE vuông tại C và ΔBDE vuông tại D có
EA=EB
\(\widehat{AEC}=\widehat{BED}\)
Do đó: ΔACE=ΔBDE
Suy ra: EC=ED
Ta có: AE+ED=AD
BE+CE=BC
mà AE=BE
và ED=EC
nên AD=BC
6 tháng 12 2021
Bài 12:
a: Xét ΔABM và ΔACN có
AB=AC
\(\widehat{ABM}=\widehat{ACN}\)
BM=CN
Do đó: ΔABM=ΔACN
TN
1
10 tháng 1 2022
a/ Tam giác AMN cân tại A (gt). \(\Rightarrow\) \(\widehat{AMN}=\widehat{ANM};AM=AN.\)
Xét tam giác AMB và tam giác ANC có:
+ AM = AN (cmt).
+ \(\widehat{AMB}=\widehat{ANC}\left(\widehat{AMN}=\widehat{ANM}\right).\)
+ MB = NC (gt).
\(\Rightarrow\) Tam giác AMB = Tam giác ANC (c - g - c).
\(\Rightarrow\) AB = AC (cặp cạnh tương ứng).
Xét tam giác ABC có: AB = AC (cmt).
\(\Rightarrow\) Tam giác ABC cân tại A.
b/ Tam giác ABC cân tại A (cmt) \(\Rightarrow\) \(\widehat{ABC}=\widehat{ACB}.\)
Mà \(\widehat{ABC}=\widehat{MBH;}\widehat{ACB}=\widehat{NCK}\text{}\) (đối đỉnh).
\(\Rightarrow\) \(\widehat{MBH}=\widehat{NCK}.\)
Xét tam giác MBH và tam giác NCK \(\left(\widehat{BHM}=\widehat{CKN}=90^o\right)\)có:
+ MB = NC (gt).
+ \(\widehat{MBH}=\widehat{NCK}\left(cmt\right).\)
\(\Rightarrow\) Tam giác MBH = Tam giác NCK (cạnh huyền - góc nhọn).
c/ Tam giác MBH = Tam giác NCK (cmt).
\(\Rightarrow\) \(\widehat{BMH}=\widehat{CNK}\) (cặp góc tương ứng).
Xét tam giác OMN có: \(\widehat{NMO}=\widehat{MNO}\) (do \(\widehat{BMH}=\widehat{CNK}\)).
\(\Rightarrow\) Tam giác OMN tại O.
H
mn ơi giúp em, nhanh ạ, chỉ cần làm đến bài 2 thôi,bài 1 chỉ cần làm đến câu 17
2
20 tháng 10 2021
Bài 6:
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{a}{41}=\dfrac{b}{29}=\dfrac{c}{30}=\dfrac{a+b}{41+29}=\dfrac{700}{70}=10\)
Do đó: a=410; b=290; c=300
S
2
25 tháng 7 2023
`@` `\text {Ans}`
`\downarrow`
`1,`
`a)`
\(\dfrac{x}{2}=\dfrac{y}{3}\text{ và }x+y=50\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
`x/2 = y/3 = (x+y)/(2 + 3) = 50/5 = 10`
`=> x/2 = y/3 = 10`
`=> x = 10*2 = 20; y = 3*10 = 30`
Vậy, `x = 20; y = 30`
`b)`
\(\dfrac{x}{2}=\dfrac{y}{3}\text{ và }5x+4y=110\)
Ta có:
`x/2 = y/3` `=> (5x)/10 = (4y)/12`
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
`(5x)/10 = (4y)/12 = (5x+4y)/(10 + 12) = 110/22 = 5`
`=> x/2 = y/3 = 5`
`=> x = 2*5 = 10; y = 3*5 = 15`
Vậy, `x = 10; y = 15`
`c)`
\(5x=11y\text{ và }2x+3y=37\)
Ta có:
`5x = 11y -> x/11 = y/5 -> (2x)/22 = (3y)/15`
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
`(2x)/22 = (3y)/15 = (2x+3y)/(22+15) = 37/37 = 1`
`=> x/11 = y/5 = 1`
`=> x = 11; y = 5`
Vậy, `x = 11; y = 5`
`d)`
\(\dfrac{x}{2}=\dfrac{y}{1}\text{và }x+y-63=0\)
Ta có: `x + y - 63 = 0 -> x + y = 63`
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
`x/2 = y/1 = (x+y)/(2+1) = 63/3 = 21`
`=> x/2 = y/1 = 21`
`=> x = 21*2 =42; y = 21`
Vậy, `x = 42; y = 21.`
NN
25 tháng 7 2023
`2,`
`a)`
\(\dfrac{a}{14}=\dfrac{b}{2}=\dfrac{c}{4}\text{ và }a+b+c=5\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
`a/14 = b/2 = c/4 = (a+b+c)/(14+2+4)=5/20=1/4=0,25`
`=> a/14 = b/2 = c/4 = 0,25`
`=> a = 14*0,25 = 3,5` `; b = 2*0,25 = 0,5;` `c = 4*0,25 = 1`
Vậy, `a = 3,5`; `b = 0,5`; `c = 1`
`b)`
\(\dfrac{a}{3}=\dfrac{b}{5}=\dfrac{c}{8}\text{ và }7a+3b-5c=7\)
Ta có:
`a/3 = b/5 = c/8 => (7a)/21 = (3b)/15 = (5c)/40`
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
`(7a)/21 = (3b)/15 = (5c)/40 = (7a + 3b - 5c)/(21 + 15 - 40)=7/-4 = -1,75`
`=> a/3 = b/5 = c/8 = -1,75`
`=> a = 3*(-1,75) = -5,25`
`b = 5*(-1,75) = -8,75`
`c = 8*(-1,75) = -14`
Vậy, `a = -5,25; b = -8,75`; `c = -14`
`c)`
\(\dfrac{a}{3}=\dfrac{b}{8}=\dfrac{c}{5}\text{và }3a+b-2c=14\)
Ta có:
`a/3 = b/8 = c/5 -> (3a)/9 = b/8 = (2c)/10`
Câu này bạn làm tương tự nha
`d)`
\(\dfrac{a}{3}=\dfrac{b}{2};\dfrac{b}{7}=\dfrac{c}{5}\text{ và }3a+5c-7b=30\)
Ta có:
`a/3 = b/2 -> a/21 = b/14`/
`b/7 = c/5 -> b/14 = c/10`
`=> a/21 = b/14 = c/10`
`=> (3a)/63 = (7b)/98 = (5c)/50`
Câu này bạn cũng làm tương tự.
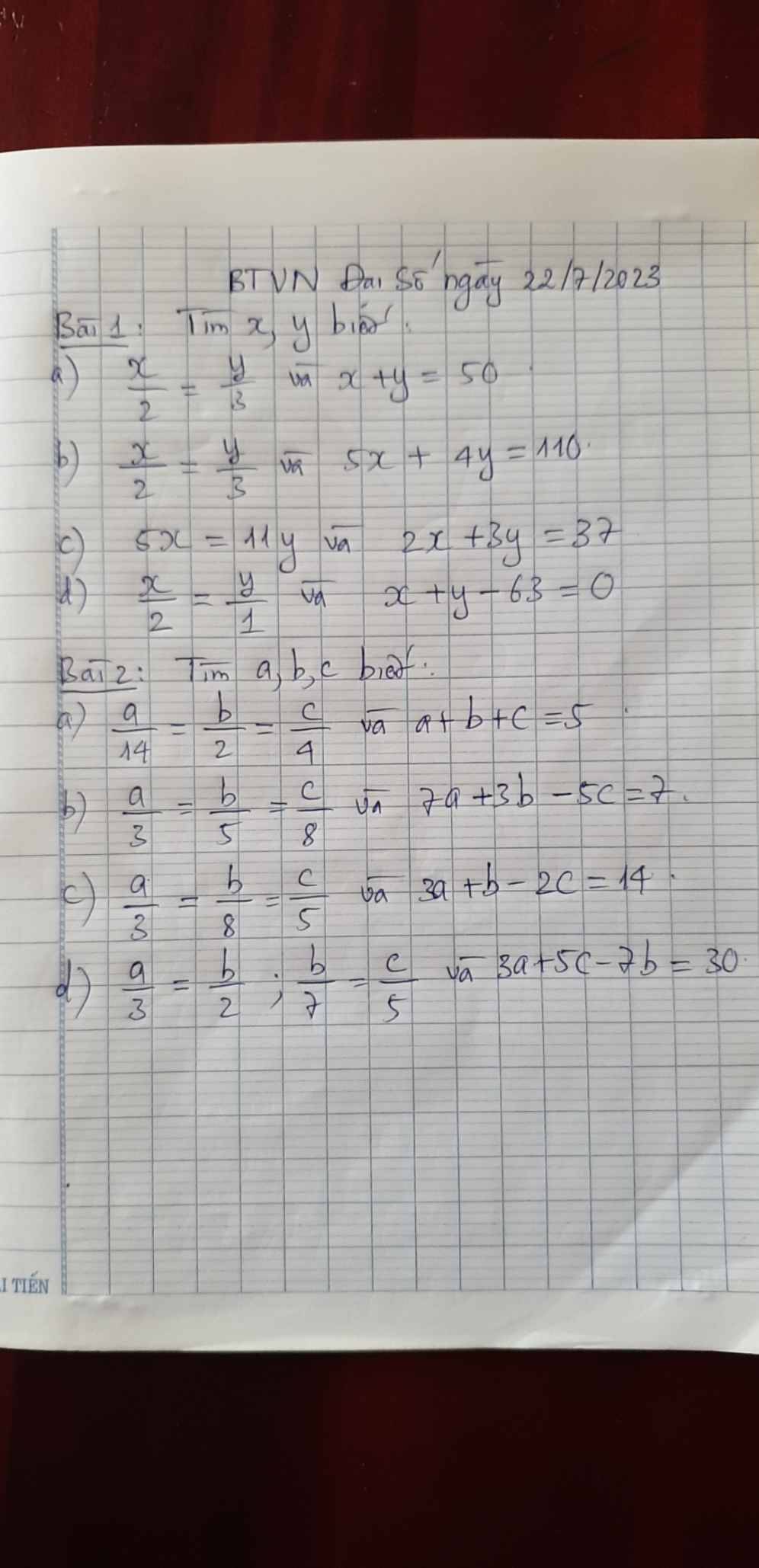
a, Theo định lí Pytago tam giác ABC vuông tại A
\(BC=AB^2+AC^2=5cm\)
b, Xét tam giác ABD và tan giác EBD có
BD _ chung
^ABD = ^EBD
Vậy tam giác ABD = tam giác EBD (ch-gn)
c, AD = ED ( 2 cạnh tương ứng )
Xét tam giác IAD và tam giác CED có
^IDA = ^CDE ( đ . đ )
AD = ED ( cmt )
Vậy tam giác IAD = tam giác CED (ch-cgv)
=> ID = CD ( 2 cạnh tương ứng )
Xét tam giác IDC có
ID = DC => tam giác IDC cân tại D