K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NL
1
17 tháng 10 2021
Bài 7:
a: \(A=x+\sqrt{x}\ge0\forall x\)
Dấu '=' xảy ra khi x=0
T
3 tháng 10 2023
\(a,P=\dfrac{\sqrt{x}}{\sqrt{x}-1}+\dfrac{3}{\sqrt{x}+1}-\dfrac{6\sqrt{x}-4}{x-1}\left(x\ge0;x\ne1\right)\)
\(=\dfrac{\sqrt{x}\left(\sqrt{x}+1\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}+\dfrac{3\left(\sqrt{x}-1\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}-\dfrac{6\sqrt{x}-4}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{x+\sqrt{x}+3\sqrt{x}-3-6\sqrt{x}+4}{\left(\sqrt{x}-1\right)\left(\sqrt{x} +1\right)}\)
\(=\dfrac{x-2\sqrt{x}+1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{\left(\sqrt{x}-1\right)^2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{\sqrt{x}-1}{\sqrt{x}+1}\)
\(---\)
\(b,P< \dfrac{1}{2}\Leftrightarrow\dfrac{\sqrt{x}-1}{\sqrt{x}+1}< \dfrac{1}{2}\)
\(\Leftrightarrow\dfrac{\sqrt{x}-1}{\sqrt{x}+1}-\dfrac{1}{2}< 0\)
\(\Leftrightarrow\dfrac{2\left(\sqrt{x}-1\right)}{2\left(\sqrt{x}+1\right)}-\dfrac{\sqrt{x}+1}{2\left(\sqrt{x}+1\right)}< 0\)
\(\Leftrightarrow\dfrac{2\sqrt{x}-2-\sqrt{x}-1}{2\left(\sqrt{x}+1\right)}< 0\)
\(\Leftrightarrow\dfrac{\sqrt{x}-3}{2\left(\sqrt{x}+1\right)}< 0\)
\(\Leftrightarrow\sqrt{x}-3< 0\left(vì.2\left(\sqrt{x}+1\right)>0\forall x\ge0\right)\)
\(\Leftrightarrow\sqrt{x}< 3\)
\(\Leftrightarrow x< 9\)
Kết hợp với điều kiện của \(x\), ta được:
\(0\le x< 9;x\ne1\) thì \(P< \dfrac{1}{2}\)
#\(Toru\)
V
0
V
0
11 tháng 12 2023
Bài 8:
a: Xét tứ giác AEHF có
\(\widehat{AEH}=\widehat{AFH}=\widehat{FAE}=90^0\)
=>AEHF là hình chữ nhật
=>AH=FE
Xét ΔAMN vuông tại A có AH là đường cao
nên \(AH^2=HM\cdot HN\)
=>\(FE^2=HM\cdot HN\)
b: Ta có: AEHF là hình chữ nhật
=>\(\widehat{AFE}=\widehat{AHE}\)
mà \(\widehat{AHE}=\widehat{M}\left(=90^0-\widehat{HAM}\right)\)
nên \(\widehat{AFE}=\widehat{M}\)
Ta có; ΔAMN vuông tại A
mà AD là đường trung tuyến
nên DN=DA
=>\(\widehat{DAN}=\widehat{DNA}\)
Ta có: \(\widehat{AFE}+\widehat{DAN}\)
\(=\widehat{DNA}+\widehat{M}\)
\(=90^0\)
=>AD\(\perp\)FE
KV
3 tháng 10 2023
Bài 6
Ta có:
sin²x + cos²x = 1
⇒ cos²x = 1 - sin²x
= 1 - 1/9
= 8/9
⇒ cosx = 2√2/3
⇒ tanx = sinx : cosx
= 1/3 : 22/3
= √2/4
⇒ cotx = 1 : tanx
= 1 : √2/4
= 2√2
H9
HT.Phong (9A5)
CTVHS
4 tháng 10 2023
Bài 2:
Ta có:
\(A=\dfrac{\sqrt{x}+1}{\sqrt{x}-3}=\dfrac{\sqrt{x}-3+4}{\sqrt{x}-3}=1+\dfrac{4}{\sqrt{x}-3}\)
A nhận giá trị nguyên khi \(\dfrac{4}{\sqrt{x}-3}\) nguyên:
\(\Rightarrow4\) ⋮ \(\sqrt{x}-3\)
\(\Rightarrow\sqrt{x}-3\inƯ\left(4\right)=\left\{1;-1;2;-2;4;-4\right\}\)
Mà: \(\sqrt{x}-3\ge-3\)
\(\Rightarrow\sqrt{x}-3\in\left\{1;-1;2;-2;4\right\}\)
\(\Rightarrow\sqrt{x}\in\left\{4;2;5;1;7\right\}\)
\(\Rightarrow x\in\left\{16;4;25;1;49\right\}\)
T
3 tháng 10 2023
\(A=\dfrac{\sqrt{x}-5}{\sqrt{x}+2}=\dfrac{\sqrt{x}+2-7}{\sqrt{x}+2}=1-\dfrac{7}{\sqrt{x}+2}\) (ĐK: \(x\ge0\))
Để \(A\) nhận giá trị nguyên thì \(1-\dfrac{7}{\sqrt{x}+2}\) nhận giá trị nguyên
\(\Rightarrow\dfrac{7}{\sqrt{x}+2}\) nhận giá trị nguyên
\(\Rightarrow\sqrt{x}+2\inƯ\left(7\right)\)
\(\Rightarrow\sqrt{x}+2\in\left\{1;7;-1;-7\right\}\)
\(\Rightarrow\sqrt{x}\in\left\{-1;5;-3;-9\right\}\) mà \(\sqrt{x}\ge0\forall x\ge0\)
\(\Rightarrow\sqrt{x}=5\)
\(\Rightarrow x=25\left(tmdk\right)\)
#\(Toru\)
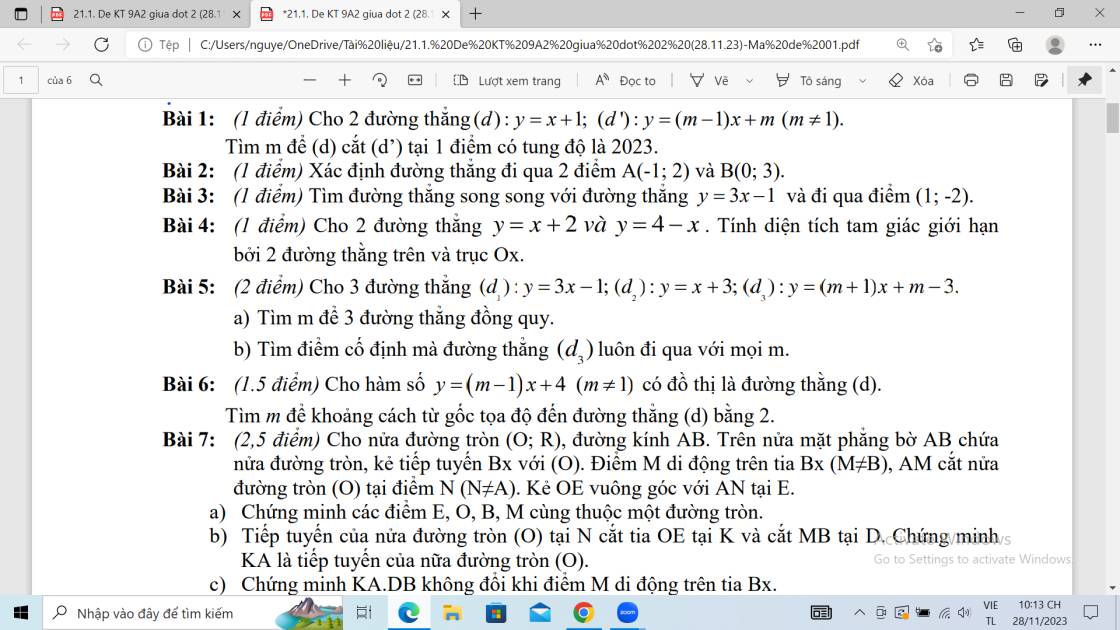
Bài 7:
a: Xét tứ giác EOBM có
\(\widehat{OEM}+\widehat{OBM}=90^0+90^0=180^0\)
=>EOBM là tứ giác nội tiếp
=>E,O,B,M cùng thuộc một đường tròn
b: ΔAON cân tại O
mà OK là đường cao
nên OK là phân giác của góc AON
Xét ΔOAK và ΔONK có
OA=ON
\(\widehat{AOK}=\widehat{NOK}\)
OK chung
Do đó: ΔOAK=ΔONK
=>\(\widehat{OAK}=\widehat{ONK}=90^0\)
=>KA là tiếp tuyến của (O)
c: Xét (O) có
DN,DB là tiếp tuyến
Do đó: DN=DB và OD là phân giác của góc NOB
=>\(\widehat{NOB}=2\cdot\widehat{NOD}\)
\(\widehat{NOA}+\widehat{NOB}=180^0\)(hai góc kề bù)
\(\Leftrightarrow2\cdot\widehat{KON}+2\cdot\widehat{NOD}=180^0\)
=>\(2\cdot\widehat{KOD}=180^0\)
=>\(\widehat{KOD}=90^0\)
Xét ΔKOD vuông tại O có ON là đường cao
nên \(NK\cdot ND=ON^2\)
mà NK=KA và ND=DB
nên \(KA\cdot DB=ON^2=R^2\) không đổi
Bài 1:
Thay y=2023 vào y=x+1, ta được:
x+1=2023
=>x=2022
Thay x=2022 và y=2023 vào (d'), ta được:
\(2022\left(m-1\right)+m=2023\)
=>2022m-2022+m=2023
=>2023m=4045
=>\(m=\dfrac{4045}{2023}\)