
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) \(y' = \left( {{x^3} - 3{x^2} + 4} \right)' = 3{x^2} - 6x\), \(y'\left( 2 \right) = {3.2^2} - 6.2 = 0\)
Thay \({x_0} = 2\) vào phương trình \(y = {x^3} - 3{x^2} + 4\) ta được: \(y = {2^3} - {3.2^2} + 4 = 0\)
Ta có phương trình tiếp tuyến của đồ thị hàm số: \(y = 0.(x - 2) + 0 = 0\)
Vậy phương trình tiếp tuyến của đồ thị hàm số là y = 0
b) \(y' = \left( {\ln x} \right)' = \frac{1}{x}\), \(y'(e) = \frac{1}{e}\)
Thay \({x_0} = e\) vào phương trình \(y = \ln x\) ta được: \(y = \ln e = 1\)
Ta có phương trình tiếp tuyến của đồ thị hàm số: \(y = \frac{1}{e}.\left( {x - e} \right) + 1 = \frac{1}{e}x - 1 + 1 = \frac{1}{e}x\)
Vậy phương trình tiếp tuyến của đồ thị hàm số là: \(y = \frac{1}{e}x\)
c) \(y' = \left( {{e^x}} \right)' = {e^x},\,\,y'(0) = {e^0} = 1\)
Thay \({x_0} = 0\) vào phương trình \(y = {e^x}\) ta được: \(y = {e^0} = 1\)
Ta có phương trình tiếp tuyến của đồ thị hàm số: \(y = 1.\left( {x - 0} \right) + 1 = x + 1\)
Vậy phương trình tiếp tuyến của đồ thị hàm số là: \(y = x + 1\)

Ta thấy ^EHK = ^EHM + ^KHM = ^BAE + ^CAM = ^BAC = 900
Đường thẳng HE: đi qua \(H\left(2;2\right)\), VTPT \(\overrightarrow{HK}\left(1;-1\right)\Rightarrow\) \(HE:x-y=0\)
Xét hệ \(\hept{\begin{cases}x-y=0\\x+y-6=0\end{cases}\Leftrightarrow\hept{\begin{cases}x=3\\y=3\end{cases}}}\Rightarrow E\left(3;3\right)\)
Đường thẳng KE: đi qua \(K\left(3;1\right)\), VTCP \(\overrightarrow{KE}\left(0;2\right)\Rightarrow KE:\hept{\begin{cases}x=3\\y=1+2t\end{cases}}\)
Xét hệ \(\hept{\begin{cases}2x-y-2=0\\x=3\\y=1+2t\end{cases}}\Leftrightarrow\hept{\begin{cases}x=3\\y=4\end{cases}}\Rightarrow A\left(3;4\right)\)
Đường thẳng BC: đi qua \(H\left(2;2\right)\), VTPT \(\overrightarrow{HA}\left(1;2\right)\Rightarrow BC:x+2y-6=0\)(1)
Đường thẳng EB: đi qua \(E\left(3;3\right)\), VTPT \(\overrightarrow{KE}\left(0;2\right)\Rightarrow BE:y=3\)(2)
Đường thẳng KC: đi qua \(K\left(3;1\right)\), VTPT \(\overrightarrow{KE}\left(0;2\right)\Rightarrow KC:y=1\) (3)
Từ (1);(2) suy ra \(B\left(0;3\right)\), từ (1);(3) suy ra \(C\left(4;1\right)\)
Vậy \(A\left(3;4\right),B\left(0;3\right),C\left(4;1\right).\)

1: cos(3x-45 độ)=0
=>3x-45 độ=90 độ+k*180 độ
=>3x=135 độ+k*180 độ
=>x=45 độ+k*60 độ
=45 độ-120 độ+(k+2)*60 độ
=-75 độ+z*60 độ
=>Chọn B
2;
tan(x-15 độ)=1
=>x-15 độ=45 độ+k*180 độ
=>x=60 độ+k*180 độ
=>Chọn C
3: 2*cos(4x-20 độ)=0
=>cos(4x-20 độ)=0
=>4x-20 độ=90 độ+k*180 độ
=>4x=110 độ+k*180 độ
=>x=27,5 độ+k*45 độ
=>Chọn C

Để giải các phương trình này, chúng ta cần sử dụng các quy tắc và công thức của hàm tan và hàm cot. Hãy xem cách giải từng phương trình một:
a) Để giải phương trình tan(x) = -1, ta biết rằng giá trị của hàm tan là -1 tại các góc -π/4 và 3π/4. Vì vậy, x có thể là -π/4 + kπ hoặc 3π/4 + kπ, với k là số nguyên.
b) Để giải phương trình tan(x+20°) = tan(60°), ta có thể sử dụng quy tắc tan(A+B) = (tanA + tanB) / (1 - tanAtanB). Áp dụng công thức này, ta có: (tanx + tan20°) / (1 - tanxtan20°) = tan60°. Giải phương trình này, ta sẽ tìm được giá trị của x.
c) Để giải phương trình tan(3x) = tan(x-π/6), ta có thể sử dụng quy tắc tan(A-B) = (tanA - tanB) / (1 + tanAtanB). Áp dụng công thức này, ta có: (tan3x - tan(π/6)) / (1 + tan3xtan(π/6)) = 0. Giải phương trình này, ta sẽ tìm được giá trị của x.
d) Để giải phương trình tan(5x+π/4) = 0, ta biết rằng giá trị của hàm tan là 0 tại các góc π/2 + kπ, với k là số nguyên. Vì vậy, 5x+π/4 = π/2 + kπ. Giải phương trình này, ta sẽ tìm được giá trị của x.
e) Để giải phương trình cot(2x-π/4) = 0, ta biết rằng giá trị của hàm cot là 0 tại các góc π + kπ, với k là số nguyên. Vì vậy, 2x-π/4 = π + kπ. Giải phương trình này, ta sẽ tìm được giá trị của x.
a: tan x=-1
=>tan x=tan(-pi/4)
=>x=-pi/4+kpi
b: tan(x+20 độ)=tan 60 độ
=>x+20 độ=60 độ+k*180 độ
=>x=40 độ+k*180 độ
c: tan 3x=tan(x-pi/6)
=>3x=x-pi/6+kpi
=>2x=-pi/6+kpi
=>x=-pi/12+kpi/2
d: tan(5x+pi/4)=0
=>5x+pi/4=kpi
=>5x=-pi/4+kpi
=>x=-pi/20+kpi/5
e: cot(2x-pi/4)=0
=>2x-pi/4=pi/2+kpi
=>2x=3/4pi+kpi
=>x=3/8pi+kpi/2

a, \(cos^2x-cosx=0\)
\(\Leftrightarrow cosx\left(cosx-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cosx=0\\cosx=1\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{2}+k\pi\\x=0\end{matrix}\right.\)
b, \(2sin2x+\sqrt{2}sin4x=0\)
\(\Leftrightarrow2sin2x+2\sqrt{2}sin2x.cos2x=0\)
\(\Leftrightarrow sin2x\left(1+\sqrt{2}cos2x\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sin2x=0\\1+\sqrt{2}cos2x=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}2x=k\pi\\cos2x=-\dfrac{\sqrt{2}}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{k\pi}{2}\\2x=\dfrac{3\pi}{4}+k2\pi\\2x=\dfrac{\pi}{4}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{k\pi}{2}\\x=\dfrac{3\pi}{8}+k\pi\\x=\dfrac{\pi}{8}+k\pi\end{matrix}\right.\)
a, \(cos^2x-cosx=0\)
\(\Leftrightarrow cosx\left(cosx-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cosx=0\\cosx=1\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{2}+k\pi\\x=k2\pi\end{matrix}\right.\) (k ∈ Z)
Vậy...
b, \(2sin2x+\sqrt{2}sin4x=0\)
\(\Leftrightarrow2sin2x+2\sqrt{2}sin2x.cos2x=0\)
\(\Leftrightarrow2sin2x\left(1+\sqrt{2}cos2x\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sin2x=0\\cos2x=\dfrac{-\sqrt{2}}{2}\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}2x=k\pi\\2x=\pm\dfrac{3\pi}{4}+k2\pi\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{k\pi}{2}\\x=\pm\dfrac{3\pi}{8}+k\pi\end{matrix}\right.\)
Vậy...
c, \(8cos^2x+2sinx-7=0\)
\(\Leftrightarrow8\left(1-sin^2x\right)+2sinx-7=0\)
\(\Leftrightarrow8sin^2x-2sinx-1=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sinx=\dfrac{1}{2}\\sinx=-\dfrac{1}{4}\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{6}+k2\pi\\x=\dfrac{5\pi}{6}+k2\pi\\x=arcsin\left(-\dfrac{1}{4}\right)+k2\pi\\x=\pi-arcsin\left(-\dfrac{1}{4}\right)+k2\pi\end{matrix}\right.\)
Vậy...
d, \(4cos^4x+cos^2x-3=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cos^2x=\dfrac{3}{4}\\cos^2x=-1\left(loai\right)\end{matrix}\right.\)
\(\Leftrightarrow\dfrac{cos2x+1}{2}=\dfrac{3}{4}\)
\(\Leftrightarrow cos2x=\dfrac{1}{2}\)
\(\Leftrightarrow2x=\pm\dfrac{\pi}{3}+k2\pi\)
\(\Leftrightarrow x=\pm\dfrac{\pi}{6}+k\pi\)
Vậy...
e, \(\sqrt{3}tanx-6cotx+\left(2\sqrt{3}-3\right)=0\) (ĐK: \(x\ne\dfrac{k\pi}{2}\))
\(\Leftrightarrow\sqrt{3}tanx-\dfrac{6}{tanx}+\left(2\sqrt{3}-3\right)=0\)
\(\Leftrightarrow\sqrt{3}tan^2x+\left(2\sqrt{3}-3\right)tanx-6=0\)
\(\Leftrightarrow\left[{}\begin{matrix}tanx=\sqrt{3}\\tanx=-2\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{3}+k\pi\left(tm\right)\\x=arctan\left(-2\right)+k\pi\end{matrix}\right.\)
Vậy...
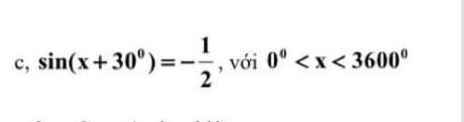
Lời giải:
$\sin (x+30^0)=\frac{-1}{2}=\sin (-30^0)$
\(\Rightarrow \left[\begin{matrix} x+30^0=-30^0+360^0k\\ x+30^0=210^0+360^0k\end{matrix}\right.\) với $k$ nguyên
\(\Leftrightarrow \left[\begin{matrix} x=-60^0+360^0k(1)\\ x=180^0+360^0k(2)\end{matrix}\right.\)
Với $(1): $0^0< -60^0+360^0k< 3600^0$
$\Leftrightarrow \frac{1}{6}< k< 10$
Mà $k$ nguyên nên $k=1;2;3;...;9$. Bạn thay các giá trị này vô $(1)$ để tìm $x$
Với $(2): $0^0< 180^0+360^0k< 3600^0$
$\Leftrightarrow \frac{-1}{2}< k< 9,5$. Mà $k$ nguyên nên $k=0,1,2,..,9$. Bạn thay các giá trị này vô $(2)$ để tìm $x$