Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Cách dựng:
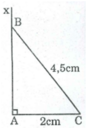
- Dựng đoạn AC = 2cm.
- Dựng góc ∠ (CAx) bằng 90 0
- Dựng cung tròn tâm C bán kính 4,5cm cắt Ax tại B. Nối CB ta có ΔABC cần dựng .
Chứng minh:
∆ ABC có ∠ A = 90 0 , AC = 2 cm, BC = 4,5 cm.
Thỏa mãn điều kiện bài toán.

a) Phân tích:
Giả sử dựng được ΔABC thỏa mãn yêu cầu.
Ta dựng được đoạn BC vì biết BC = 2cm.
Khi đó điểm A là giao điểm của:
+ Tia Bx vuông góc với BC
+ Cung tròn tâm C bán kính 4cm.
b) Cách dựng:
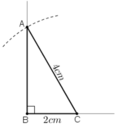
+ Dựng đoạn thẳng BC = 2cm.
+ Dựng tia Bx vuông góc với cạnh BC.
+ Dựng cung tròn tâm C, bán kính 4cm. Cung tròn cắt tia Bx tại A.
Kẻ AC ta được ΔABC cần dựng.
c) Chứng minh
ΔABC có góc B = 90º, BC = 2cm.
A thuộc cung tròn tâm C bán kính 4cm nên AC = 4cm.
Vậy ΔABC thỏa mãn yêu cầu đề bài
d) Biện luận: Ta luôn dựng được một hình thang thỏa mãn điều kiện của đề bài.

a) Phân tích:
Giả sử dựng được ΔABC thỏa mãn yêu cầu.
Ta dựng được đoạn BC vì biết BC = 2cm.
Khi đó điểm A là giao điểm của:
+ Tia Bx vuông góc với BC
+ Cung tròn tâm C bán kính 4cm.
b) Cách dựng:
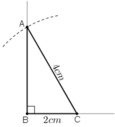
+ Dựng đoạn thẳng BC = 2cm.
+ Dựng tia Bx vuông góc với cạnh BC.
+ Dựng cung tròn tâm C, bán kính 4cm. Cung tròn cắt tia Bx tại A.
Kẻ AC ta được ΔABC cần dựng.
c) Chứng minh
ΔABC có góc B = 90º, BC = 2cm.
A thuộc cung tròn tâm C bán kính 4cm nên AC = 4cm.
Vậy ΔABC thỏa mãn yêu cầu đề bài
d) Biện luận: Ta luôn dựng được một hình thang thỏa mãn điều kiện của đề bài.

giả sử ta đã có tam giác ABC vuông tại B
áp dụng định lí py-ta-go vào tam giác ABC vuông tại B có:
BC2+AB2=AC2
22+AB2=42
4+AB2=16
AB2=12
=>AB=\(\sqrt{12}\)(cm)
Các bước vẽ :
B1: vẽ đoạn thẳng AC = 4cm
B2: dùng com-pa vẽ một đường tròn tâm A bán kính 2 cm
B3: dùng com-pa vẽ một đường tròn tâm AB bán kính \(\sqrt{12}cm\)
B4 : 2 đường tròn cắt nhau tại một điểm điểm đó là B nói 3 điểm A;B;C lại với nhau ta được tam giác ABC vuông tại B có cạnh huyền AC=4cm cạnh góc vuông BC=2cm
bài này cần 4 bước:
- Phân tích
- dựng hình
- chứng minh
-biện luận

Gọi độ dài cạnh góc vuông còn lại là x
=>ĐỘ dài cạnh huyền là x+3
THeo đề, ta có: x^2+25=(x+3)^2
=>x^2+6x+9=x^2+25
=>6x=16
=>x=8/3
=>\(S=\dfrac{8}{3}\cdot3\cdot\dfrac{1}{2}=4\left(cm^2\right)\)

a) Phân tích
Giả sử dựng được ΔABC thỏa mãn yêu cầu đề bài.
Đoạn thẳng BC dựng được vì đã biết độ dài.
Khi đó điểm A là giao điểm của:
+ Tia Bx tạo với đoạn thẳng BC góc 65º
+ Đường thẳng qua C và vuông góc với tia Bx vừa dựng.
b) Cách dựng:
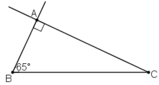
- Dựng đoạn thẳng BC = 4cm.
- Dựng tia Bx tạo với BC một góc 65º.
- Dựng đường thẳng a qua C và vuông góc với Bx.
- Bx cắt a tại A.
ΔABC là tam giác cần dựng.
c) Chứng minh: ΔABC vừa dựng vuông tại A, góc B = 65º và BC = 4cm.
d) Biện luận: Ta luôn dựng được một tam giác thỏa mãn điều kiện đề bài.