Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Xét các trường hợp:
1. a, b, a’, b’ ≠ 0
Ta có:
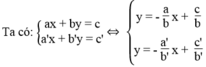
Hệ phương trình có vô số nghiệm khi hai đường thẳng trùng nhau. Nghĩa là hai đường thẳng có hệ số góc và tung độ gốc bằng nhau:
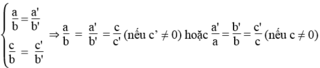
*a = 0, a’ ≠ 0
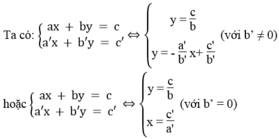
Vì hai đường thẳng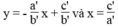 
luôn luôn cắt trục hoành còn đường thẳng y = c/b song song hoặc trùng với trục hoành nên chúng luôn luôn cắt nhau.
Vậy hệ phương trình chỉ có một nghiệm duy nhất.
*a = a’ = 0
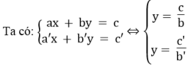
Hệ có vô số nghiệm khi hai đường thẳng trùng nhau, nghĩa là:
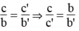
Hệ vô nghiệm khi hai đường thẳng song song nhau, nghĩa là:
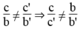
*b = 0, b’ ≠ 0
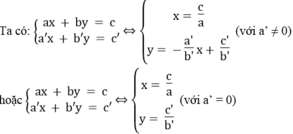
Vì hai đường thẳng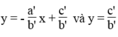 
luôn luôn cắt trục tung còn đường thẳng x = c/a song song hoặc trùng với trục tung nên chúng luôn luôn cắt nhau.
Vậy hệ phương trình chỉ có một nghiệm duy nhất.
*b = b’ = 0
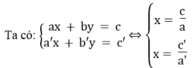
Hệ có vô số nghiệm khi hai đường thẳng trùng nhau, nghĩa là:
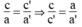
Hệ vô nghiệm khi hai đường thẳng song song nhau, nghĩa là:
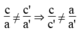
Áp dụng:
Hệ hai phương trình bậc nhất hai ẩn có vô số nghiệm:
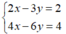
Vì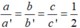 
nên hệ phương trình có vô số nghiệm
Xét các trường hợp:
1. a, b, a’, b’ ≠ 0
Ta có:
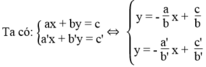
Hệ phương trình vô nghiệm khi hai đường thẳng song song nhau. Nghĩa là hai đường thẳng có hệ số góc bằng nhau và tung độ gốc khác nhau:
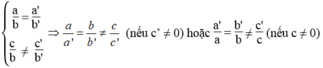
Áp dụng:
Hệ hai phương trình bậc nhất hai ẩn vô nghiệm:
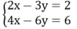
Vì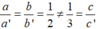 
nên hệ phương trình trên vô nghiệm
Xét các trường hợp:
1. a, b, a’, b’ ≠ 0
Ta có:
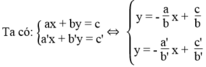
Hệ phương trình có một nghiệm duy nhất khi hai đường thẳng cắt nhau. Nghĩa là hai đường thẳng có hệ số góc khác nhau:
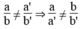
Áp dụng:
Hệ hai phương trình bậc nhất hai ẩn vô nghiệm:
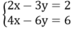
Vì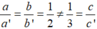 
nên hệ phương trình trên vô nghiệm
Ta biết tập nghiệm của phương trình ax + by = c được biểu diễn bằng đường thẳng ax + by = c và tập nghiệm của phương trình a'x + b'y = c' được biểu diễn bằng đường thẳng a'x + b'y = c'.
Ta biết tập nghiệm của phương trình ax + by = c được biểu diễn bằng đường thẳng ax + by = c và tập nghiệm của phương trình a'x + b'y = c' được biểu diễn bằng đường thẳng a'x + b'y = c'.
a) Hệ đã cho vô nghiệm bởi vì mỗi nghiệm của hệ là nghiệm chung của hai phương trình, một phương trình vô nghiệm thì hệ không có nghiệm chung.
b) Hệ đã cho có vô số nghiệm.
Xét hệ phương trình bậc nhất hai ẩn a x + b y = c a ' x + b ' y = c ' (các hệ số khác 0)
- Hệ phương trình có nghiệm duy nhất ⇔ a a ' ≠ b b '
- Hệ phương trình vô nghiệm ⇔ a a ' = b b ' ≠ c c '
- Hệ phương trình có vô số nghiệm ⇔ a a ' = b b ' = c c '
Đáp án: B