Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Trong bảng phân bố (tần số hoặc tần suất) ghép lớp, tần suất của lớp thứ i được kí hiệu là f i i và bằng:
f i = n i / n = n i / n . 100 . 1 / 100 = n i / n . 100 % .
Trong đó, n i là tần số của lớp thứ i, n là số tất cả các số liệu thống kê đã cho.
Trong bài toán đã cho, ta có:
f 3 = 14/63 = 0,(2);
Làm tròn đến hàng phần trăm ta có: f 3 ≈ 0,22 = 0,22.100% = 22%.

a) Năm 2010:
Tỉ lệ hộ nghèo trung bình là:
\(\overline {{x_{2010}}} = \frac{{5,3 + 10,4 + 7,0 + ... + 10,0 + 12,2}}{{10}} = 9,6\)
Phương sai của mẫu số liệu năm 2010 là:
\({s_{2010}}^2 = \frac{1}{{10}}\left[ {{{(5,3 - 9,6)}^2} + {{(10,4 - 9,6)}^2} + ... + {{(12,2 - 9,6)}^2}} \right] = 5,308\)
\( \Rightarrow \) Độ lệch chuẩn là \({s_{2010}} = \sqrt {{s_{2010}}^2} = \sqrt {5,308} \approx 2,304\)
Năm 2016:
Tỉ lệ hộ nghèo trung bình là:
\(\overline {{x_{2016}}} = \frac{{1,3 + 2,9 + 1,6 + ... + 3,0 + 4,3}}{{10}} = 2,82\)
Phương sai của mẫu số liệu năm 2016 là:
\({s_{2016}}^2 = \frac{1}{{10}}\left[ {{{(1,3 - 2,82)}^2} + {{(2,9 - 2,82)}^2} + ... + {{(4,3 - 2,82)}^2}} \right] = 1,0136\)
\( \Rightarrow \) Độ lệch chuẩn là \({s_{2016}} = \sqrt {{s_{2016}}^2} = \sqrt {1,0136} \approx 1,007\)
b) Theo số trung bình thì tỉ lệ hộ nghèo các tỉnh/ thành phố thuộc đồng bằng sông Hồng của năm 2016 giảm khoảng 3,4 lần so với năm 2010.
Theo độ lệch chuẩn, độ phân tán của tỉ lệ hộ nghèo các tỉnh/ thành phố thuộc đồng bằng sông Hồng của năm 2016 nhỏ hơn 2010, từ đó cho thấy sự chênh lệch về tỉ lệ hộ nghèo giữa các tỉnh/ thành phố năm 2016 là nhỏ hơn so với năm 2010.

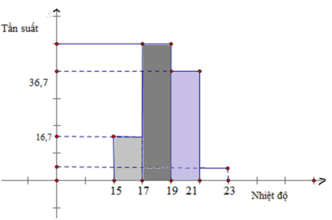
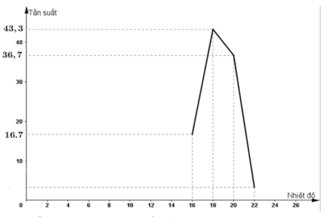
a) Bảng 6:
| Lớp nhiệt độ (ºC) | Tần suất (%) | Giá trị đại diện |
| [15; 17] | 16,7 | 16 |
| [17; 19) | 43,3 | 18 |
| [19; 21) | 36,7 | 20 |
| [21; 23] | 3,3 | 22 |
| Cộng | 100 (%) |
Số trung bình cộng của bảng 6 là:
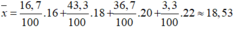
Số trung bình cộng của bảng 8 là:
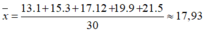
b) Nhiệt độ trung bình của thành phố Vinh trong tháng 12 cao hơn nhiệt độ trung bình trong tháng 2 khoảng 0,6ºC.

• Ta có:
- Số trung bình cộng x = 55,82 trường là không có nghĩa.
- Trong các số liệu thống kê đã cho có sự chênh lệch quá lớn (điều này chứng tỏ các số liệu thống kê đã cho là không cùng loại)
Chỉ cần một trong hai điều kể trên là đủ để suy ra rằng: Không chọn được số trung bình cộng làm đại diện cho các số liệu thống kê.
• Dễ thấy: Bảng số liệu thống kê đã cho không có mốt.
• Trong trường hợp đã cho, ta chọn số trung vị M e = 40 (trường) để làm đại diện cho các số liệu thống kê đã cho (về quy mô và độ lớn).
Đáp án: B

a) Tỉ lệ thành phố có thuế thuốc lá lớn hơn 36 là tỉ lệ thành phố có thuế thuốc lá lớn hơn \({Q_1}\)
=> Có 75%
b) Ta thấy từ giá trị nhỏ nhất đến \({Q_2}\) có 50% giá trị của mẫu số liệu nằm giữa hai giá trị này
=> Ta chọn giá trị thứ nhất là 2,5 và 36.
c) Khoảng tứ phân vị \({\Delta _Q} = {Q_3} - {Q_1} = 100 - 36 = 64\)

a)
Tỉnh Thái Bình:
Số trung bình \(\overline x = \frac{{1061,9 + 1061,9 + 1053,6 + 942,6 + 1030,4}}{5} = 1030,08\)
Phương sai \({S^2} = \frac{1}{5}\left( {1061,{9^2} + 1061,{9^2} + 1053,{6^2} + 942,{6^2} + 1030,{4^2}} \right) - 1030,{08^2} = 2046,2\)
=> Độ lệch chuẩn \(S = \sqrt {{S^2}} \approx 45,2\)
+) Khoảng biến thiên \(R = 1061,9 - 942,6 = 119,3\)
Tỉnh Hậu Giang:
Số trung bình \(\overline x = \frac{{1204,6 + 1293,1 + 1231,0 + 1261,0 + 1246,1}}{5} = 1247,16\)
Phương sai \({S^2} = \frac{1}{6}\left( {1204,{6^2} + 1293,{1^2} + 1231,{0^2} + 1261,{0^2} + 1246,{1^2}} \right) - 1247,{16^2} = 875,13\)
=> Độ lệch chuẩn \(S = \sqrt {{S^2}} \approx 29,6\)
+) Khoảng biến thiên \(R = 1293,1 - 1204,6 = 88,5\)
b)
So sánh khoảng biến thiên và độ lệch chuẩn ta đều thấy tỉnh Hậu Giang có sản lượng lúa ổn định hơn.

Biểu đồ hình cột thể hiện nhiệt độ trung bình của thành phố Vinh.
Biểu đồ hình gấp khúc thể hiện nhiệt độ trung bình của thành phố Vinh.

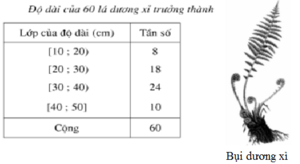
a) Bảng phân bố tần suất ghép lớp:
| Lớp của chiều dài (cm) | Tần suất |
|---|---|
| [10; 20) | 13,3 |
| [20; 30) | 30,0 |
| [30; 40) | 40,0 |
| [40; 50) | 16,7 |
| Cộng | 100 (%) |
b) Tỉ lệ lá có chiều dài dưới 30 cm là:
13,3 + 30 = 43,3 %
Tỉ lệ lá có chiều dài từ 30 cm đến 50 cm là:
40 + 16,7 = 56,7 %

Điểm số của xạ thủ A có:
x ≈ 8 , 3 đ i ể m , s 1 2 ≈ 1 , 6 ; s 1 ≈ 1 , 27 .
Điểm số của xạ thủ B có
y ≈ 8 , 4 đ i ể m , s 2 2 ≈ 1 , 77 ; s 2 ≈ 1 , 27 .





80% là giá trị đại diện của lớp thứ năm – lớp [70; 90) (của bảng 8), nên có thể xem các số liệu thống kê thuộc vào lớp thứ năm đều bằng 80%. Suy ra: Số các tỉnh, thành phố có “tỉ lệ các trường mần non đạt chuẩn quốc gia trong năm học 2013 – 2014” từ 30% đến 80% là: 14 + 5 + 2 = 21 (tỉnh, thành phố)
Đáp án: D