Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, \(CH_4+2O_2\underrightarrow{t^o}CO_2+H_2O\)
\(2C_2H_2+5O_2\underrightarrow{t^o}4CO_2+2H_2O\)
Ta có: \(n_{CH_4}+n_{C_2H_2}=\dfrac{33,6}{22,4}=1,5\left(mol\right)\left(1\right)\)
Theo PT: \(n_{CO_2}=n_{CH_4}+2n_{C_2H_2}=\dfrac{56}{22,4}=2,5\left(mol\right)\left(2\right)\)
Từ (1) và (2) \(\Rightarrow\left\{{}\begin{matrix}n_{CH_4}=0,5\left(mol\right)\\n_{C_2H_2}=1\left(mol\right)\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}\%V_{CH_4}=\dfrac{0,5.22,4}{33,6}.100\%\approx33,33\%\\\%V_{C_2H_2}\approx66,67\%\end{matrix}\right.\)
b, Theo PT: \(n_{O_2}=2n_{CH_4}+\dfrac{5}{2}n_{C_2H_2}=3,5\left(mol\right)\Rightarrow m_{O_2}=3,5.32=112\left(g\right)\)

Gọi \(\left\{{}\begin{matrix}n_{CO}=a\left(mol\right)\\n_{C_nH_{2n+2}}=b\left(mol\right)\end{matrix}\right.\)
=> \(a+b=\dfrac{4,48}{22,4}=0,2\left(mol\right)\)
Bảo toàn C: \(a+bn=\dfrac{5,6}{22,4}=0,25\left(mol\right)\)
Bảo toàn H: \(2bn+2b=\dfrac{2,7}{18}.2=0,3\left(mol\right)\)
=> a = 0,15; b = 0,05; n = 2
=> CTPT: C2H6
\(\left\{{}\begin{matrix}\%V_{C_2H_6}=\dfrac{0,05}{0,2}.100\%=25\%\\\%V_{CO}=\dfrac{0,15}{0,2}.100\%=75\%\end{matrix}\right.\)

Giả sử các khí đo ở điều kiện sao cho 1 mol khi có thể tích V lít
\(n_{CO}+n_{CO_2}=\dfrac{20}{V}\)
\(n_{O_2}=\dfrac{8}{V}\left(mol\right)\)
PTHH: 2CO + O2 --to--> 2CO2
_____\(\dfrac{16}{V}\)<---\(\dfrac{8}{V}\)
=> \(\left\{{}\begin{matrix}n_{CO}=\dfrac{16}{V}\\n_{CO_2}=\dfrac{20}{V}-\dfrac{16}{V}=\dfrac{4}{V}\end{matrix}\right.\)
=> \(\left\{{}\begin{matrix}\%V_{CO}=\dfrac{\dfrac{16}{V}}{\dfrac{20}{V}}.100\%=80\%\\\%V_{CO_2}=\dfrac{\dfrac{4}{V}}{\dfrac{20}{V}}.100\%=20\%\end{matrix}\right.\)

Chọn nCO2 = 6 , nH2O = 7
Hỗn hợp Y gồm nO2 = a mol, nO3 = b mol
X + Y → CO2 + H2O
Áp dụng ĐLBT nguyên tố O: 2a + 3b = 6.2 + 7
mY = 32a + 48b = 19.2 (a+b)
=> a = 5 và b = 3
=> nX = 1/2 nY = 4 mol
=> mX = 6.44 + 7.18 - 32.5 - 48.3 = 83 gam
<=> MX = \(\dfrac{m_X}{n_X}\)= 20,75 gam/mol
<=> d\(\dfrac{X}{H_2}\)= 20,75:2 = 10,375

Vì bài toán chỉ có số liệu tương đối (%) nên để đơn giản và không mất tính tổng quát, ta có thể chọn số mol một chất bất kì. Ta chọn nX = 1(mol)
![]()
Khi làm lạnh thì hơi nước ngưng tụ vậy Y chỉ chứa CO2 và O2 dư.
Pt:
CxHy + (x + 0,25y)O2 → xCO2 + 0,5yH2O
a → a(x + 0,25y) ax 0,5ay
dư: 1 – a – a(x + 0,25y)

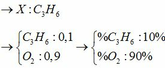

a, \(CH_4+2O_2\underrightarrow{t^o}CO_2+2H_2O\)
\(2C_2H_2+5O_2\underrightarrow{t^o}4CO_2+2H_2O\)
Ta có: \(n_{CH_4}+n_{C_2H_2}=\dfrac{6,72}{22,4}=0,3\left(mol\right)\left(1\right)\)
\(n_{CO_2}=n_{CH_4}+2n_{C_2H_2}=\dfrac{7,84}{22,4}=0,35\left(mol\right)\left(2\right)\)
Từ (1) và (2) \(\Rightarrow\left\{{}\begin{matrix}n_{CH_4}=0,25\left(mol\right)\\n_{C_2H_2}=0,05\left(mol\right)\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}\%V_{CH_4}=\dfrac{0,25.22,4}{6,72}.100\%\approx83,33\%\\\%V_{C_2H_2}\approx16,67\%\end{matrix}\right.\)
Theo PT: \(n_{O_2}=2n_{CH_4}+\dfrac{5}{2}n_{C_2H_2}=0,625\left(mol\right)\Rightarrow m_{O_2}=0,625.32=20\left(g\right)\)
\(Coi\ n_B = 1(mol) \\ n_{CO_2} = 1.30\% =0,3(mol) ; n_{H_2O} = 1.20\% = 0,2(mol)\\ A: C_nH_{2n+2-2k}\\\ n_C = n_{CO_2} = 0,3(mol)\\ n_H = 2n_{H_2O} = 0,4(mol)\\ Ta có : \dfrac{n}{2n+2-2k} = \dfrac{0,3}{0,4}\\ \Leftrightarrow 0,4n = 0,6n + 0,6 - 0.6k\\ \Leftrightarrow 0,6k -0,2n = 0,6\\ \Leftrightarrow 6k - 2n = 6\)
Với k = 1 thì n = 0(loại)
Với k = 2 thì n = 3(chọn)
Với k = 3 thì n = 6(chọn)
.....
Vậy hidrocacbon có thể là : \(C_3H_4 ; C_6H_8,...\)
\(Coi\ n_B = 1(mol)\\ \Rightarrow n_{CO_2} = 1.30\% = 0,3(mol) ; n_{H_2O} = 20\% = 0,2(mol) ; n_{O_2} = 50% = 0,5(mol)\)
Vì \(n_{CO_2} > n_{H_2O} \Rightarrow A: C_nH_{2n-2}\)
\(n_A = n_{CO_2} - n_{H_2O} = 0,3 - 0,2 = 0,1(mol)\\ \Rightarrow n = \dfrac{n_{CO_2}}{n_A} = \dfrac{0,2}{0,1} = 2\\ CTPT\ A: C_2H_2\)