Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ở đây có bài tương tự nè
http://olm.vn/hoi-dap/thanh-vien/titanic123


Độ dài cung tạo bởi mũi kim giờ và kim phút lúc đồng hồ chỉ điểm 5 giờ là:
\(\dfrac{5}{12}\times30=12,5\left(cm\right)\)
(Nếu khó quá em vặn đồng hồ về nhà mình xem thử hè)

Thời gian của vòi lớn là
\(1\div20=\frac{1}{20}\) giờ
Thời gian của vòi nhỏ là
\(1\div9=\frac{1}{9}\) giờ
Thời gian chảy của cả hai vòi là
\(\frac{1}{9}+\frac{1}{20}=\frac{29}{180}\) giờ
Nếy chảy riêng thì hết số thời gian là
\(1\div\frac{29}{180}=\frac{180}{29}\) giờ
Đổi \(\frac{180}{90}\) giờ \(=\) 2 giờ
Đáp số 2 giờ
Chúc bạn học giỏi
Mình nhầm nhé
Kết quả cuối cùng bằng \(\frac{180}{29}\)
Chúc bạn học giỏi

Gọi 2 đường trung bình của hình vuông (do hình vuông cũng là hình thang) lần lượt là MN và EF.
Trên MN lấy 2 điểm P,Q sao cho MN = 3MP = 3NQ (như hình vẽ):
Gọi R, S là giao điểm của một đường thẳng bất kì đi qua P và cắt hai cạnh của hình vuông.
Ta có: \(S_{ARSD}=\frac{\left(AR+DS\right).AD}{2};S_{BRSC}=\frac{\left(BR+CS\right).BC}{2}=\frac{\left(BR+CS\right).AD}{2}\)
Vì MP là đường trung bình của hình thang ARSD, NP là đường trung bình của hình thang BRSC
\(\Rightarrow MP=\frac{AR+DS}{2};NP=\frac{BR+CS}{2}\)
\(\Rightarrow S_{ARSD}=AD.MP;S_{BRSC}=AD.NP\)
Ta lại có: MN = 3 MP
\(\Rightarrow MN-MP=2MP\)
\(\Rightarrow NP=2MP\)
\(\Rightarrow S_{ARSD}=0,5.S_{BRSQ}\)(Ta được một đường thẳng thỏa mãn đề bài)
Chứng minh tương tự, ta có đường thẳng đi qua Q cũng thỏa mãn yêu cầu của đề bài. Suy ra từ một đường trung bình sẽ có 2 điểm nằm trên nó mà các đường thẳng đi qua nó cắt 2 cạnh của tam giác thỏa mãn yêu cầu đề bài. Mà hình vuông có 2 đường trung bình nên sẽ có 4 điểm mà các đường thẳng đi qua thỏa mãn các tính chất trên.
Vì vậy, các đường thẳng thỏa mãn muốn thỏa mãn yêu cầu đề bài phải đi qua 1 trong 4 điểm trên.
Ta lại có: 2005 : 4 = 501 (dư 1)
Theo nguyên lí Dirichlet, có ít nhất 502 đường thẳng đồng quy tại 1 trong số 4 điểm. Bài toán được chứng mình.
- Các đường thẳng đã cho không thể cắt các cạnh kề nhau của hình vuông, bởi vì nếu thế chúng chia hình vuông thành một tam giác và ngũ giác (chứ không phải chia hình vuông thành hai tứ giác)
- Do đó, mỗi đường thẳng (trong số chín đường thẳng) đều cắt hai cạnh đối của hình vuông và không đi qua một đỉnh nào của hình vuông cả.
- Giả sử một đường thẳng cắt hai cạnh đối và tại các điểm M và N
Ta có: \(\frac{S_{ABMN}}{S_{MCND}}\)= \(\frac{1}{2}\) <=> \(\frac{EJ}{JF}\)= \(\frac{1}{2}\)
(ở đây E và F là các trung điểm của AB và CD tương ứng)
- Gọi E, F, P, Q tương ứng là các trung điểm của AB, CD, BC, AD. Gọi là các điểm sao cho nằm trên nằm trên và thỏa mãn:
\(\frac{EJ_1}{J_1F}=\frac{FJ_2}{J_2P}=\frac{PJ_3}{J_3Q}=\frac{QJ_4}{J_4E}=\frac{1}{2}\)
-Khi đó từ đó lập luận trên ta suy ra mỗi đường thẳng có tính chất thỏa mãn yêu cầu của đề bài phải đi qua một trong 4 điểm nói trên. -Vì có 2005 đường thẳng, nên theo nguyên lý Dirichle phải tồn tại ít nhất một trong 4 điểm sao cho nó có ít nhất [2005:4]+1=502 trong 2005 đường thẳng đã cho đi qua
Vậy có ít nhất 502 đường thẳng trong 2005 đường thẳng đã cho đi qua một điểm.

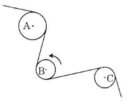
Từ hình vẽ, đường tròn (A) và (C) nằm cùng một phía (về bên dưới) so với sợi dây nên có cùng chiều quay, còn đường tròn (B) nằm ở khác phía (bên trên).
=> đường tròn (A) và (C) quay ngược chiều với (B).
Khi dây cua-roa chuyển động, đường tròn (B) quay ngược chiều của kim đồng hồ nên đường tròn (A) và (C) có cùng chiều quay của kim đồng hồ.
45 phút nhé bạn kb và k mik nha
duoc 45 phut