Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi thời gian chảy của vòi thứ nhất để bể đầy là a giờ (a > 0)
\(\Rightarrow\)Thời gian chảy của vòi thứ 2 để bể đầy là a + 2 giờ
Đổi : 2 giờ 24 phút : = \(\frac{12}{5}\) giờ
\(\Rightarrow\)Nếu cả 2 vòi cùng chảy thì sau một giờ nước trong bể sẽ bằng : \(\frac{1}{\frac{12}{5}}=\frac{5}{12}\)(bể)
Ta có phương trình :
\(\frac{1}{a}+\frac{1}{a+2}=\frac{5}{12}\)
\(\Leftrightarrow\frac{12\left(a+2\right)+12a}{12a\left(a+2\right)}=\frac{5a\left(a+2\right)}{12a\left(a+2\right)}\)
\(\Leftrightarrow12a+24+12a=5a^2+10a\)
\(\Leftrightarrow-5a^2+14a+24=0\)
\(\Leftrightarrow-5a^2-6a+20a+24=0\)
\(\Leftrightarrow-a\left(5a+6\right)+4\left(5a+6\right)=0\)
\(\Leftrightarrow\left(5a+6\right)\left(4-a\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}5a+6=0\\4-a=0\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}a=-\frac{6}{5}\left(ktm\right)\\a=4\left(tm\right)\end{cases}}\)
Vậy thời gian vòi thứ nhất chảy 1 mình để đầy bể là 4 giờ
thời gian vòi thứ 2 chảy 1 mình để đầy bể là 4 + 2 = 6 giờ.

Gọi thời gian vòi 1 chảy một mình đẩy bể là x ( x<4)
Gọi thời gian vòi 2 chảy một mình đầy bể là y (y<4)
Trong một giờ:
-Vòi 1 chảy một mình được \(\dfrac{1}{x}\)(bể)
-Vòi 2 chảy được \(\dfrac{1}{y}\)(bể)
-Cả hai vòi chảy được \(\dfrac{1}{4}\)(bể)
+Ta có PT: \(\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{9}\) (1)
Vì nếu để vòi 1 chảy một mình trong 30 phút rồi khóa lại và mở vòi hai trong 20 phút thì cả hai vòi chảy được 1/9 bể nên có PT:
\(\dfrac{1}{2}x+\dfrac{1}{3}y=\dfrac{1}{9}\)
⇔\(\dfrac{x}{2}+\dfrac{y}{3}=\dfrac{1}{9}\) (2)
Từ (1) và (2) ta có HPT: \(\left\{{}\begin{matrix}\dfrac{x}{1}+\dfrac{y}{1}=\dfrac{1}{4}\\\dfrac{x}{2}+\dfrac{y}{3}=\dfrac{1}{9}\end{matrix}\right.\)
⇔\(\left\{{}\begin{matrix}x=6\\y=12\end{matrix}\right.\)(TM)
Vậy vòi 1 chảy một mình trong 6 giờ thì đẩy bể
Vậy vòi 2 chảy một mình trong 12 giờ thì đẩy bể

Gọi x(giờ) là thời gian vòi 1 chảy một mình đầy bể
y(giờ) là thời gian vòi 2 chảy một mình đầy bể
(Điều kiện: x>3; y>3)
Trong 1 giờ, vòi 1 chảy được: \(\dfrac{1}{x}\)(bể)
Trong 1 giờ, vòi 2 chảy được: \(\dfrac{1}{y}\)(bể)
Trong 1 giờ, hai vòi chảy được: \(\dfrac{1}{3}\)(bể)
Do đó, ta có phương trình: \(\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{3}\)(1)
Vì khi mở vòi 1 trong 20' và mở vòi 2 trong 30' thì cả hai vòi chảy được 1/8 bể nên ta có phương trình:
\(\dfrac{1}{3x}+\dfrac{1}{2y}=\dfrac{1}{8}\)(2)
Từ (1) và (2) ta lập được hệ phương trình:
\(\left\{{}\begin{matrix}\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{3}\\\dfrac{1}{3}\cdot\dfrac{1}{x}+\dfrac{1}{2}\cdot\dfrac{1}{y}=\dfrac{1}{8}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{1}{3}\cdot\dfrac{1}{x}+\dfrac{1}{3}\cdot\dfrac{1}{y}=\dfrac{1}{9}\\\dfrac{1}{3}\cdot\dfrac{1}{x}+\dfrac{1}{2}\cdot\dfrac{1}{y}=\dfrac{1}{8}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{-1}{6}\cdot\dfrac{1}{y}=\dfrac{-1}{72}\\\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{3}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{1}{y}=\dfrac{1}{12}\\\dfrac{1}{x}+\dfrac{1}{12}=\dfrac{1}{3}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{1}{x}=\dfrac{1}{3}-\dfrac{1}{12}=\dfrac{1}{4}\\\dfrac{1}{y}=\dfrac{1}{12}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=4\\y=12\end{matrix}\right.\)(thỏa ĐK)
Vậy: Vòi 1 cần 4 giờ để chảy một mình đầy bể
Vòi 2 cần 12 giờ để chảy một mình đầy bể

Lời giải:
Đổi 20 phút = $\frac{1}{3}$ giờ; 30 phút = $\frac{1}{2}$ giờ
Giả sử vòi 1 và vòi 2 chảy 1 mình thì sau tương ứng $a,b$ giờ thì đầy bể
Khi đó, trong 1 giờ thì:
Vòi 1 chảy $\frac{1}{a}$ bể; vòi 2 chảy $\frac{1}{b}$ bể
Theo bài ra ta có: \(\left\{\begin{matrix} \frac{3}{a}+\frac{3}{b}=1\\ \frac{1}{3a}+\frac{1}{2b}=\frac{1}{8}\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} \frac{1}{a}=\frac{1}{4}\\ \frac{1}{b}=\frac{1}{12}\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} a=4\\ b=12\end{matrix}\right.\)
Vậy......

Gọi x (phút), y (phút) lần lượt là thời gian vòi thứ nhất, vòi thứ hai chảy một mình để đầy bể.
(Điều kiện: x, y > 80 )
Trong 1 phút vòi thứ nhất chảy được 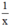 bể; vòi thứ hai chảy được
bể; vòi thứ hai chảy được 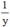 bể.
bể.
Sau 1 giờ 20 phút = 80 phút, cả hai vòi cùng chảy thì đầy bể nên ta có phương trình:
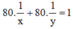
Mở vòi thứ nhất trong 10 phút và vòi thứ 2 trong 12 phút thì chỉ được 2/15 bể nước nên ta có phương trình :
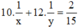
Ta có hệ phương trình:
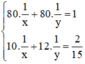
Đặt 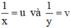 . Khi đó hệ phương trình trở thành :
. Khi đó hệ phương trình trở thành :
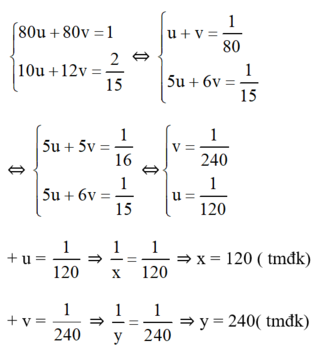
Vậy nếu chảy một mình, để đầy bể vòi thứ nhất chảy trong 120 phút (= 2 giờ) , vòi thứ hai 240 phút (= 4 giờ)

Gọi x (phút), y (phút) lần lượt là thời gian vòi thứ nhất, vòi thứ hai chảy một mình để đầy bể.
(Điều kiện: x, y > 80 )
Trong 1 phút vòi thứ nhất chảy được 1/x bể; vòi thứ hai chảy được 1/y bể.
Sau 1 giờ 20 phút = 80 phút, cả hai vòi cùng chảy thì đầy bể nên ta có phương trình:
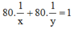
Mở vòi thứ nhất trong 10 phút và vòi thứ 2 trong 12 phút thì chỉ được 2/15 bể nước nên ta có phương trình :
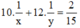
Ta có hệ phương trình:
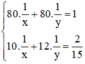
Đặt 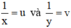 . Khi đó hệ phương trình trở thành :
. Khi đó hệ phương trình trở thành :
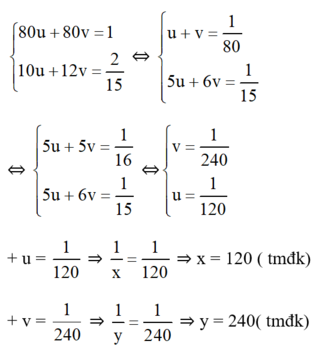
Vậy nếu chảy một mình, để đầy bể vòi thứ nhất chảy trong 120 phút (= 2 giờ) , vòi thứ hai 240 phút (= 4 giờ)
Kiến thức áp dụng
Giải bài toán bằng cách lập hệ phương trình :
Bước 1 : Lập hệ phương trình
- Chọn các ẩn số và đặt điều kiện thích hợp
- Biểu diễn các đại lượng chưa biết và đã biết theo ẩn
- Lập các phương trình biểu thị mối quan hệ giữa các đại lượng theo đề bài.
- Từ các phương trình vừa lập rút ra được hệ phương trình.
Bước 2 : Giải hệ phương trình (thường sử dụng phương pháp thế hoặc cộng đại số).
Bước 3 : Đối chiếu nghiệm với điều kiện và kết luận.

Gọi thời gian vòi một chảy một mình đến đầy bể là x (giờ) (x>0)
thời gian vòi hai chảy một mình đến đầy bể là y (giờ) (y>0)
Ta có hpt :
\(\hept{\begin{cases}\frac{1}{x}+\frac{1}{y}=\frac{1}{12}\\x=y-10\end{cases}\Leftrightarrow\hept{\begin{cases}x=20\\y=30\end{cases}\left(TM\right)}}\)
Vậy nếu chảy riêng thì vòi một chảy trong 20 giờ thì đầy bể, vòi hai chảy trong 30 giờ thì đầy bể
Thời gian của vòi lớn là
\(1\div20=\frac{1}{20}\) giờ
Thời gian của vòi nhỏ là
\(1\div9=\frac{1}{9}\) giờ
Thời gian chảy của cả hai vòi là
\(\frac{1}{9}+\frac{1}{20}=\frac{29}{180}\) giờ
Nếy chảy riêng thì hết số thời gian là
\(1\div\frac{29}{180}=\frac{180}{29}\) giờ
Đổi \(\frac{180}{90}\) giờ \(=\) 2 giờ
Đáp số 2 giờ
Chúc bạn học giỏi
Mình nhầm nhé
Kết quả cuối cùng bằng \(\frac{180}{29}\)
Chúc bạn học giỏi