Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(y'=-3x^2+6x+9\) ; \(y''=-6x+6\)
\(y''=0\Rightarrow x=1\Rightarrow y=13\)
Tâm đối xứng của đồ thị là \(\left(1;13\right)\)

y ' = - 3 x 2 - 6 x ; y ' ' = - 6 x - 6 ; y ' ' = 0 = > x = - 1
Vậy điểm U(-1; -1) là tâm đối xứng của đồ thị .
(Đồ thị hàm số bậc ba nhận điểm uốn làm tâm đối xứng – hoành độ điểm uốn là nghiệm phương trình y'' = 0 ).
Chọn đáp án A.

Đáp án B.
y' = 3x2 + 6x – 9
y’’ = 6x + 6
y’’ = 0 ó x = -1.
Thay x = -1 vào hàm số y = 12

a) TXĐ: R
📷
y’>0 trên khoảng (-∞; -2)và (0; +∞)
y'<0 trên khoảng (-2; 0)
yCĐ=y(-2)=0; yCT=y(0)=-4
📷
y”=6x+6=6(x+1)=0 <=> x = -1
Bảng xét dấu y’’
X-∞-1+∞Y’’–0+Đồ thịLồiđiểm uốn u(-1; -2)lõm
Hàm số lồi trên khoảng (-∞; -1)
Hàm số lõm trên khoảng -1; +∞)
Hàm số có 1 điểm uốn u(-1; -2)
Bảng biến thiên:
📷
Đồ thị
Đi qua điểm (1; 0) và (-3; -4)
b) Hàm số y=x3+3x2-4 có điểm uốn u(-1; -2)
Ta có: y’=3x2-4 ; y’(-1) = -3
Phương trình tiếp tuyến tại điểm uốn u(-1; -2) có dạng
y-y0=y'(x0)(x-x0)
<=> y+2=-3(x+1)
<=> y=-3x-5
Vậy phương trình tiếp tuyến tại điểm uốn là: y = -3x – 5.
📷
c) Đồ thị nhận I(-1; -2) là tâm đối xứng khi và chỉ khi:
f(x0+x)+f(x0-x)=2y0 với ∀x
<=> f(x-1)+f(-x-1)=-4 ∀x
<=> (x-1)3+3(x-1)2-4+(-1-x)3+3(-1-x)2-4 ∀x
<=> x3-3x2+3x-1+3x2-6x+3-5-3x-3x2-x3+3+6x+3x2-4=-4 ∀x
<=>-4=4 ∀x
=> I(-1; -2) là tâm đối xứng của đồ thị.
bạn vào chính câu hỏi này của bạn trong bingbe xem

Đáp án B.
Số điểm chung là số nghiệm phân biệt của phương trình hoành độ:
-x3 + 3x2 + 2x – 1 = 3x2 – 2x – 1 => x3 – 4x = 0 => x = 0; x = ±2
Phương trình có 3 nghiệm phân biệt nên số điểm chung là 3

+ Đồ thi hàm số đã cho co TCĐ là : x= -1 và TCN là y= 1; tâm đối xứng- giao của 2 đườg tiệm cận có tọa độ là I ( -1; 1)
Gọi M x 0 ; x 0 - 2 x 0 + 1 ∈ C , x 0 ≠ - 1 , I ( - 1 ; 1 )
+ Phương trình tiếp tuyến tại M có dạng
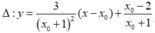
+ Giao điểm của ∆ với tiệm cận đứng là A - 1 ; x 0 - 5 x 0 + 1
+ Giao điểm của ∆ với tiệm cận ngang là B( 2x0+1; 1).
Ta có 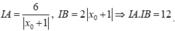
Bán kính đường tròn ngoại tiếp tam giác IAB là S=p.r, suy ra
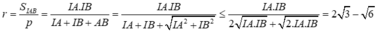
Suy ra,
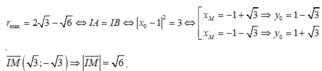
Chọn D.

Chọn D
y ' = 3 x 2 + 6 x + m 2 . Hàm số có hai điểm cực trị => y’=0 có hai nghiệm phân biệt <=> Δ ' = 3 2 - 3 . m 2 > 0 <=> - 3 < m < 3
Chia y cho y’ ta được:
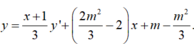
Giả sử x 1 , x 2 là hai nghiệm phân biệt của y’=0.
Phương trình đường thẳng đi qua hai điểm cực trị có dạng
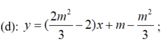
(d) có vectơ pháp tuyến là
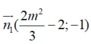

Vì hai điểm cực trị đối xứng với nhau qua (Δ) nên (d) ⊥ (Δ)
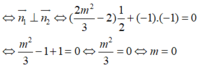
Thử lại khi m=0 ta có: y = x 3 + 3 x 2 ; y ' = 3 x 2 + 6 x ; y ' ' = 6 x + 6
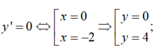
y''(0) = 6 > 0; y''(-2) = -6 < 0
Tọa độ hai điểm cực trị của đồ thị hàm số là O(0;0), A(-2;4)
Trung điểm của OA là I(-1;2).
Ta thấy I(-1,2) không thuộc đường thẳng (Δ) . Vậy không tồn tại m.