Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Chọn A
Đk để hàm số xác định là: 
. Vậy mệnh đề 
đúng.
Do hàm số có tập xác định 
nên không tồn tại 
do đó đồ thị hàm số này không có đường tiệm cận ngang. Vậy mệnh đề 
sai.
Do 
nên đồ thị hàm số có 
đường tiệm cận đứng là 
và 
. Vậy 
đúng.
Ta có
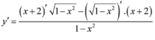
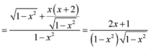
Do 
bị đổi dấu qua 
nên hàm số có một cực trị. Vậy mệnh đề 
đúng.
Do đó số mệnh đề đúng là 
.
1.
\(\lim\limits_{x\rightarrow\infty}\frac{3x-2}{x+1}=3\Rightarrow y=3\) là tiệm cận ngang
2.
\(\lim\limits_{x\rightarrow2}\frac{-2x}{x-2}=\infty\Rightarrow x=2\) là tiệm cận đứng
3.
\(\lim\limits_{x\rightarrow\infty}\frac{x-2}{x^2-1}=0\Rightarrow y=0\) là tiệm cận ngang
4.
\(\lim\limits_{x\rightarrow\infty}\frac{x-1}{x^2-x}=0\Rightarrow y=0\) là tiệm cận ngang
\(\lim\limits_{x\rightarrow0}\frac{x-1}{x^2-x}=\infty\Rightarrow x=0\) là tiệm cận đứng
\(\lim\limits_{x\rightarrow1}\frac{x-1}{x^2-x}=1\) hữu hạn nên \(x=1\) ko phải tiệm cận đứng
ĐTHS có 2 tiệm cận
