Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

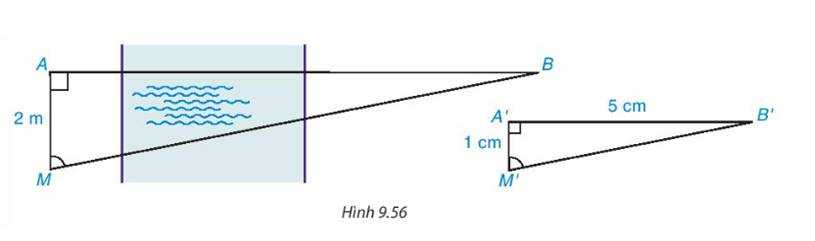
Xét ΔA′M′B′ (vuông tại A) và ΔAMB (vuông tại A') có \(\widehat {A'M'B'} = \widehat {AMB}\)
=> ΔA′M′B′ ∽ ΔAMB
=> \(\frac{{A'M'}}{{AM}} = \frac{{A'B'}}{{AB}}\)
=> \(\frac{1}{2} = \frac{5}{{AB}}\)
=> AB=10 (cm)

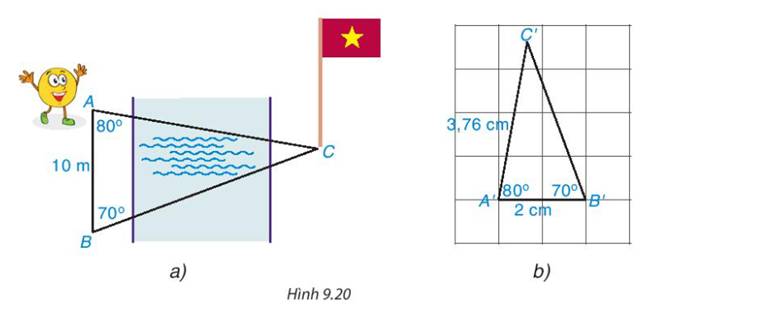
Tam giác A'B'C' đồng dạng với tam giác ABC với tỉ số đồng dạng \(\frac{1}{5}\)

Vì tam giác A’B’C’ đồng dạng với tam giác ABC theo tỉ số \(\frac{1}{{1\,000\,000}}\) nên ta có:
\(\begin{array}{l}\frac{{A'B'}}{{AB}} = \frac{{B'C'}}{{BC}} = \frac{{A'C'}}{{AC}} = \frac{1}{{1\,000\,000}}\\ \Rightarrow \frac{4}{{AB}} = \frac{5}{{BC}} = \frac{6}{{AC}} = \frac{1}{{1\,000\,000}}\end{array}\)
\( \Rightarrow \)AB = 4 000 000cm = 40km.
\( \Rightarrow \)BC = 5 000 000cm = 50km.
\( \Rightarrow \)AC = 6 000 000cm = 60km.
Vậy khoảng cách giữa A và B là 40km, khoảng cách giữa B và C là 50km, khoảng cách giữa C và A là 60km.

Lời giải:
a) Ta thấy:
$\frac{4}{8}=\frac{5}{10}=\frac{6}{12}$ nên 2 tam giác đồng dạng theo TH c.c.c
b) Pitago: $A'C'=\sqrt{B'C'^2-A'B'^2}=\sqrt{16^2-9^2}=5\sqrt{7}$
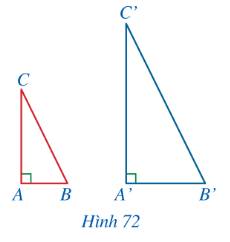
Xét tam giác $ABC$ và $A'B'C'$ có:
$\widehat{A}=\widehat{A'}=90^0$
$\frac{AB}{AC}\neq \frac{A'B'}{A'C'}$
Do đó 2 tam giác không đồng dạng

a: Xét ΔA'B'C' và ΔABC có
A'B'/AB=A'C'/AC=B'C'/BC
Do đó: ΔA'B'C'\(\sim\)ΔABC
b: \(\dfrac{C_{A'B'C'}}{C_{ABC}}=\dfrac{A'B'}{AB}=2\)

Xét tam giác A’B’C’ và tam giác ABC có:
\(\frac{{A'B'}}{{AB}} = \frac{{A'C'}}{{AC}}\) và \(\widehat {A'} = \widehat A = 90^\circ \)
\( \Rightarrow \Delta A'B'C' \backsim \Delta ABC\) (c-g-c)

- Có \(\frac{{A'B'}}{{AB}} = \frac{{A'C'}}{{AC}} = \frac{2}{3}\)
- Có \(\frac{{B'C'}}{{BC}} = \frac{2}{3}\)
- Tam giác A'B'C' có đồng dạng với tam giác ABC và đồng dạng với tỉ số \(\frac{2}{3}\)

Đổi \(20m = 2000cm;\,\,50m = 5000cm\)
Ta thấy \(\frac{{A'B'}}{{AB}} = \frac{2}{{2000}} = \frac{1}{{1000}};\,\,\frac{{A'C'}}{{AC}} = \frac{5}{{5000}} = \frac{1}{{1000}}\)
\( \Rightarrow \frac{{A'B'}}{{AB}} = \frac{{A'C'}}{{AC}}\)
Xét tam giác A’B’C’ và tam giác ABC có:
\(\frac{{A'B'}}{{AB}} = \frac{{A'C'}}{{AC}}\) và \(\widehat {BAC} = \widehat {B'A'C'} = 135^\circ \)
\( \Rightarrow \Delta A'B'C' \backsim \Delta ABC\)
Khi đó
\(\begin{array}{l}\frac{{A'B'}}{{AB}} = \frac{{A'C'}}{{AC}} = \frac{{B'C'}}{{BC}} = \frac{1}{{1000}}\\ \Rightarrow \frac{{6,6}}{{BC}} \approx \frac{1}{{1000}}\\ \Rightarrow BC \approx 6600cm = 66m\end{array}\)
Vì vậy Vy có thể kết luận rằng \(B'C'\; \approx \;6,6cm\).