Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Trên cùng 1 nửa mp bờ chứa tia Ox, góc xOt = 60 độ, góc xOy = 130 độ mà xOt < xOy ( vì 60<130 ).
=> Tia Ot nằm giữa 2 tia Ox,Oy. (1)
b) => xOt + tOy = xOy
=> 60 độ + tOy = 130 độ
=> tOy = 130 độ - 60 độ = 70 độ.
c) Vì xOt = 60 độ, tOy = 70 độ. (2)
Từ (1) và (2) => tia Ot ko phải là tia phân giác của góc xOy.
Chúc bạn học giỏi ! Nhớ chọn mình nhé !

a: Vì góc xOa<góc xOb
nên tia Oa nằm giữa hai tia Ox và Ob
b: góc aOb=120-60=60 độ
=>góc xOa=góc aOb
c: Ta có: tia Oa nằm giữa haitia Ox và Ob
mà góc xOa=góc aOb
nen Oa là phân giác củagóc xOb

a)Vì tia oy và ox đều nằm trên cùng một bờ là tia ox
Suy ra: xot+toy=xoy
Do đó ot nằm giữa 2 tia ox và oy
b)Vì xot+toy=xoy
Thay số:400+toy=1100
toy=1100-400=700
Vì oz là tia phân giác góc toy
Suy ra: yoz=zot=yot:2=700:2=350
Vì ot nằm giữa góc zox
Suy ra:zot+tox=zox
Thay số:350+400=zox=750
Vậy yot=350;zox=750
c)Tia ot ko phải là tia phân giác vì theo câu b ta được
ot nằm giữa góc zox.
Mà 2 góc do tia ot tạo thành lại là hai góc ko bằng nhau
Do đó tia ot ko phải là tia phân giác

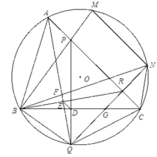
2). Gọi PQ giao BC tại D, AQ giao BR tại E ta có các biến đổi góc sau
E Q D ^ = D Q B ^ − A Q B ^ = P R B ^ − A C B ^ = R B C ^ = E B D ^ .
Vậy tứ giác BEDQ nội tiếp, suy ra B E Q ^ = B D Q ^ = 90 0 ⇒ B R ⊥ A Q

\(\widehat{DOC}=\dfrac{\widehat{AOC}}{2}\)
\(\widehat{EOC}=\dfrac{\widehat{BOC}}{2}\)
Do đó; \(\widehat{DOC}+\widehat{EOC}=\dfrac{1}{2}\left(\widehat{AOC}+\widehat{BOC}\right)\)
hay \(\widehat{DOE}=65^0\)

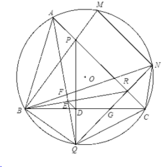
Ta có:
B P Q ^ = B R Q ^ = R B N ^ + R N B ^ = E B F ^ + B A E ^ = 90 0 − B F E ^ + 90 0 − A B E ^ = 180 0 − B F E ^ − A B E ^ = A F B ^ − A B R ^ ⇒ A F B ^ = B P Q ^ + A B R ^

Ta có: \(M{F_1} = \sqrt {{{\left( {x + c} \right)}^2} + {y^2}} ,M{F_2} = \sqrt {{{\left( {x - c} \right)}^2} + {y^2}} \).Vậy để điểm M thuộc Hyperbol khi và chỉ khi \(\left| {M{F_1} - M{F_2}} \right| = 2a\) hay\(\left| {\sqrt {{{\left( {x + c} \right)}^2} + {y^2}} - \sqrt {{{\left( {x - c} \right)}^2} + {y^2}} } \right| = 2a\)