Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn D.
Tập xác định: D = ℝ
Ta có ![]()
Xét m = 1, ta có y' = -3 < 0 ∀ x ∈ ℝ nên nghịch biến trên tập xác định.
Xét m ≠ 1 Để hàm số trên nghịch biến trên tập xác định khi và chỉ khi
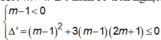
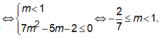
Vậy với - 2 7 ≤ m ≤ 1 thì hàm số y = ( m - 1 ) x 3 + ( m - 1 ) x 2 - ( 2 m + 1 ) + 5 nghịch biến trên tập xác định.

\(y=\dfrac{x^2-m^2+2m+1}{x-m}\) đúng không nhỉ?
\(y'=\dfrac{x^2-2mx+m^2-2m-1}{\left(x-m\right)^2}\)
Hàm đồng biến trên các khoảng xác định khi và chỉ khi:
\(x^2-2mx+m^2-2m-1\ge0\) ; \(\forall x\)
\(\Leftrightarrow\Delta'=m^2-\left(m^2-2m-1\right)\le0\)
\(\Leftrightarrow m\le-\dfrac{1}{2}\)

a) Tập xác định: D = R \ {m}
Hàm số đồng biến trên từng khoảng ( - ∞ ; m), (m; + ∞ ) khi và chỉ khi:
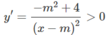
⇔ − m 2 + 4 > 0
⇔ m 2 < 4 ⇔ −2 < m < 2
c) Tập xác định: D = R
Hàm số nghịch biến trên R khi và chỉ khi:
y′ = −3 x 2 + 2mx – 3 ≤ 0
⇔ y′ = m 2 – 9 ≤ 0
⇔ m 2 ≤ 9 ⇔ −3 ≤ m ≤ 3

Hàm số
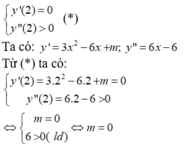
có tập xác định: D = R.
y ' = x 2 + 2 ( m + 1 ) x - m - 1
Để hàm số đã cho đồng biến trên R khi và chỉ khi:
y ' = f ( x ) = x 2 + 2 ( m + 1 ) x - m - 1 ≥ 0 ∀ x ∈ R
⇔ -2 ≤ m ≤ -1
Chọn A

a) y = –( m 2 + 5m) x 3 + 6m x 2 + 6x – 5
y′ = –3( m 2 + 5m) x 2 + 12mx + 6
Hàm số đơn điệu trên R khi và chỉ khi y’ không đổi dấu.
Ta xét các trường hợp:
+) m2 + 5m = 0 ⇔ 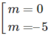
– Với m = 0 thì y’ = 6 nên hàm số luôn đồng biến.
– Với m = -5 thì y’ = -60x + 6 đổi dấu khi x đi qua .
+) Với m 2 + 5m ≠ 0. Khi đó, y’ không đổi dấu nếu
Δ' = 36 m 2 + 18( m 2 + 5m) ≤ 0 ⇔ 3 m 2 + 5m ≤ 0 ⇔ –5/3 ≤ m ≤ 0
– Với điều kiện đó, ta có –3( m 2 + 5m) > 0 nên y’ > 0 và do đó hàm số đồng biến trên R.
Vậy với điều kiện –5/3 ≤ m ≤ 0 thì hàm số đồng biến trên R.
b) Nếu hàm số đạt cực đại tại x = 1 thì y’(1) = 0. Khi đó:
y′(1) = –3
m
2
– 3m + 6 = 0 ⇔ 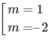
Mặt khác, y” = –6( m 2 + 5m)x + 12m
+) Với m = 1 thì y’’ = -36x + 12. Khi đó, y’’(1) = -24 < 0 , hàm số đạt cực đại tại x = 1.
+) Với m = -2 thì y’’ = 36x – 24. Khi đó, y’’(1) = 12 > 0, hàm số đạt cực tiểu tại x = 1.
Vậy với m = 1 thì hàm số đạt cực đại tại x = 1.

y = –( m 2 + 5m) x 3 + 6m x 2 + 6x – 5
y′ = –3( m 2 + 5m) x 2 + 12mx + 6
Hàm số đơn điệu trên R khi và chỉ khi y’ không đổi dấu.
Ta xét các trường hợp:
+)
m
2
+ 5m = 0 ⇔ 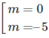
– Với m = 0 thì y’ = 6 nên hàm số luôn đồng biến.
– Với m = -5 thì y’ = -60x + 6 đổi dấu khi x đi qua .
+) Với m 2 + 5m ≠ 0. Khi đó, y’ không đổi dấu nếu
∆ ' = 36 m 2 + 18( m 2 + 5m) ≤ 0 ⇔ 3 m 2 + 5m ≤ 0 ⇔ –5/3 ≤ m ≤ 0
– Với điều kiện đó, ta có –3( m 2 + 5m) > 0 nên y’ > 0 và do đó hàm số đồng biến trên R.
Vậy với điều kiện –5/3 ≤ m ≤ 0 thì hàm số đồng biến trên R.
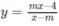 đồng biến trên từng khoảng xác định;
đồng biến trên từng khoảng xác định;
Lời giải:
a)
Hàm $y$ đồng biến trên khoảng xác định khi mà
\(y'=3x^2-6(2m+1)x+12m+5\geq 0\)
\(\Leftrightarrow \Delta'=9(2m+1)^2-3(12m+5)\leq 0\)
\(\Leftrightarrow -\sqrt{\frac{1}{6}}\leq m\leq \sqrt{\frac{1}{6}}\)
b) Hàm $y$ đồng biến trên TXĐ khi:
\(y'=3mx^2-2(2m-1)x+m-2\geq 0\) với mọi \(x\in\mathbb{R}\)
Để đảm bảo điều trên xảy ra với mọi $x$ thì \(m>0\)
Khi đó \(\Delta'=(2m-1)^2-3m(m-2)\leq 0\)
\(\Leftrightarrow (m+1)^2\leq 0\) (vô lý)
Do đó không tồn tại $m$ thỏa mãn