Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Ta có : abc x 9 = 4abc
=> abc x 9 = 4000 + abc
=> abc x 9 - abc = 4000
=> abc x (9 - 1) = 4000
=> abc x 8 = 4000
=> abc = 4000 : 8
=> abc = 500
Vậy abc = 500
Ta có:\(\overline{abc}\times9=\overline{4abc}\)
\(\overline{abc}\times9=4000+\overline{abc}\)
\(\overline{abc}\times8=4000\)
\(\overline{abc}=4000:8=500\)

4 x 1000 + abc = abc x 9
4000 = abc x 9 - abc
4000 = abc x 8
4000 : 8 = abc
500 = abc
tự đáp số

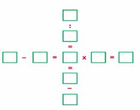
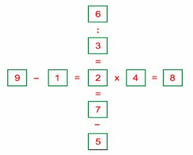
Bài toán chỉ có bốn cách điền như sau :
2 x 78 = 156 = 39 x 4
4 x 39 = 156 = 78 x 2
3 x 58 = 174 = 29 x 6
6 x 29 = 174 = 58 x 3

Đặt các chữ cái vào các ô trống:
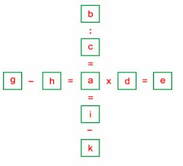
Theo đầu bài ta có các chữ cái khác nhau biểu thị các số khác nhau. Do đó: a ≠ 1; c ≠ 1; d ≠ 1; b > 1; e > 1. Vì 9 = 1 x 9 = 3 x 3 nên b ≠ 9 và e ≠ 9; và 7 = 1 x 7 nên b ≠ 7 và e ≠ 7.
Do đó: b = 6 và e = 8 hoặc b = 8 và e = 6.
Vì 6 = 2 x 3 và 8 = 2 x 4 nên a = b : c = e : d = 2.
Trong các ô trống a, b, c, d, e đã có các số 2, 3, 4, 6, 8; do đó chỉ còn các số 1, 5, 7, 9 điền vào các ô trống g, h, i, k.
* Nếu e = 6 thì g = 7 và h = 1. Do đó a = i - k = 9 - 5 = 42 (loại).
* Nếu e = 8 thì g = 9 và h = 1. Do đó a = i - k = 7 - 5 = 2 (đúng). Khi đó: b = 6 và c = 3. Kết quả:

Giải:
1ab +36 = ab1(a khác 0;a,b<10)
100+ ab +36 = ab x 10 +1
136 +ab = ab x 10 +1
135 +ab = ab x 10
ab x 9 = 135
ab = 15
Vậy ab=15
thử 115 + 36 = 151 .
B .
a b c
a c c
d b c
—----
b c c
Nhìn theo hàng đơn vị: c + c + c → c tức là c nhân 3 được một số tận cùng là c. Có 3 trường hợp:
a) 3c = c (tức là không có số nhớ) ⇒ c = 0
b) 3c = 10 + c (tức là nhớ 1) ⇒ c = 5
c) 3c = 20 + c (tức là nhớ 2) ⇒ c = 10 (loại)
(Không có TH nào khác vì 3 số có-một-chữ-số cộng lại tối đa là 27)
Nếu c = 0 (không nhớ):
----Nhìn hàng chục: b + 0 + b → 0. Tương tự trên có 3 TH:
a) 2b = 0 ⇒ b = 0 (loại vì kết quả của phép cộng là bcc nên b > 0)
b) 2b = 10 ⇒ b = 5 (nhớ 1)
c) 2b = 20 ⇒ b = 10 (loại)
----Nhìn hàng trăm: a + a + d + 1 = 5 ⇒ 2a + d = 4 ⇒ a < 4/2 = 2 ⇒ a = 1 (vì a > 0 và d > 0) ⇒ d = 2 ⇒ abcd = 1502
Nếu c = 5 (nhớ 1):
----Nhìn hàng chục: b + 5 + b + 1 → 5. Tương tự trên có 3 TH:
a) 2b + 6 = 5 ⇒ b < 0 (loại)
b) 2b + 6 = 15 ⇒ b không nguyên (loại)
c) 2b + 6 = 25 ⇒ b không nguyên (loại)
Vậy có duy nhất một số thỏa mãn đề bài là abcd = 1502 .

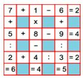
Ta đặt tên cho các số phải tìm như trong bảng. Các số điền vào ô trống là các số có 1 chữ số nên tổng các số lớn nhất chỉ có thể là 17.
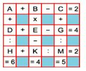
ở cột 1, có A + D : H = 6, nên H chỉ có thể lớn nhất là 2.
Cột 5 có C + G : M = 5 nên M chỉ có thể lớn nhất là 3.
* Nếu H = 1 thì A + D = 6 = 2 + 4, do đó M = 3 và H + K = 2 x 3 = 6 = 1 + 5.
K = 5 thì B x E = 4 + 5 = 9, như thế chỉ có thể B hoặc E bằng 1, điều đó chứng tỏ H không thể bằng 1.
* Nếu H = 2 thì M phải bằng 1 hoặc 3; nếu M = 1 thì H + K = 2, như vậy K = 0, điều này cũng không thể được.
Vậy M = 3 ; H + K = 6 thì K = 4.
H = 2 thì A + D = 12 = 5 + 7 ; như vậy A = 5, D = 7 hoặc D = 5, A = 7.
K = 4 thì B x E = 4 + 4 = 8 = 1 x 8 ; như vậy B = 1, E = 8 hoặc E = 1, B = 8.
M = 3 thì C + G = 15 = 6 + 9 ; như vậy C = 6, G = 9 hoặc G = 6, C = 9 ; G chỉ có thể bằng 9 vì nếu G = 6 thì D + E = 10, mà trong các số 1, 5, 7, 8 không có hai số nào có tổng bằng 10. Vậy C = 6 và A + B = 8, như vậy B chỉ có thể bằng 1, A = 7 thì D = 5 và E = 8.
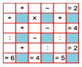
Các số điền vào bảng như hình sau.