Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

88 m
ai tk mk
mk nhất định sẽ tk lại người đó
hứa luôn
thank nhiều
Đáy phải là :
90 x 2 : 10 = 18 ( m )
Khi mở rộng đáy tam giác trái là :
22 - 18 = 4 ( m )
Diện tích mở rộng phần đất bên trái là :
4 x 10 : 2 = 20 ( m2 )
Diện tích phần được mở rộng là :
20 + 90 = 110 ( m2 )
Diện tích thửa ruộng là :
110 x 7 = 770 ( m2 )
Tổng 2 đáy là :
770 x 2 : 10 = 154 ( m )
Đáy lớn hình thang là :
( 154 + 22 ) : 2 = 88 ( m )
Đáp số : 88 m

Kẻ AH vuông góc với BC, BK vuông góc với CD, đường chéo AC vuông góc với AD.
Đặt AH = AB = x => AH = x
Tam giác AHD = tam giác BKC ( c.h - g.n)
=> DH = CK = (10-x)/2
Vậy HC = Hk + CK = x + (10-x)/2 = (x-10)/2
Áp dụng hệ thức lượng trong tam giác ADC vuông tại A
Có AH^2 = DH.HC => x^2 = (10-x)/2 . (x-10)/2
=> 5x^2 = 20
=> x = 2√ 5
Vậy AH = 2√5

Gọi a(m) là độ dài cạnh đáy nhỏ(Đk: a>0)
Độ dài cạnh đáy lớn là: a+15(m)
Theo đề, ta có phương trình:
\(\dfrac{a+a+15}{2}\cdot8=240\)
\(\Leftrightarrow\dfrac{2a+15}{2}=30\)
\(\Leftrightarrow2a+15=60\)
\(\Leftrightarrow2a=45\)
hay a=22,5(thỏa ĐK)
Vậy: Chiều dài các cạnh đáy của nó là 22,5m và 37,5m

Sửa đề: Đáy nhỏ bằng nửa đáy lớn và bằng độ dài hai cạnh bên
AB=CD/2=5cm
BD vuông góc BC
=>góc BDC+góc BCD=90 độ
AD=BC=AB=5cm
AB=AD
=>góc ABD=góc ADB
=>góc ADB=góc BDC
=>DB là phân giác của góc ADC
góc BDC+góc BCD=90 độ
=>1/2*góc BCD+góc BCD=90 độ
=>góc BCD=60 độ
=>góc BDC=30 độ
Xét ΔBDC vuông tại B có BD^2+BC^2=CD^2
=>BD=5*căn 3(cm)
Kẻ BH vuông góc CD
=>BH=BD*BC/CD=5/2*căn 3(cm)

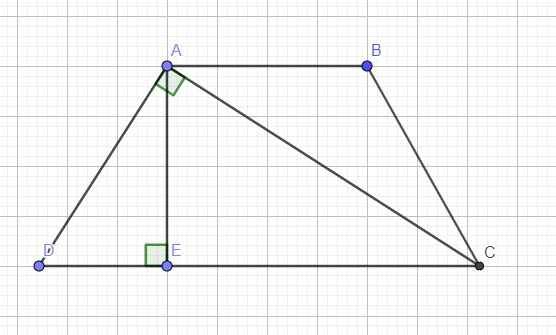
Kẻ đường cao góc AE \(\Rightarrow AE=AB\)
Lại có ABCD là hình thang cân \(\Rightarrow CD=AB+2DE=AE+2DE\Rightarrow DE=\dfrac{CD-AE}{2}=\dfrac{10-AE}{2}\)
\(EC=AB+DE=AE+DE=AE+\dfrac{10-AE}{2}=\dfrac{AE+10}{2}\)
Áp dụng hệ thức lượng trong tam giác vuông ACD có:
\(AE^2=DE.EC\Leftrightarrow AE^2=\left(\dfrac{10-AE}{2}\right)\left(\dfrac{10+AE}{2}\right)\)
\(\Leftrightarrow4AE^2=100-AE^2\Rightarrow AE=2\sqrt{5}\) \(\Rightarrow AB=2\sqrt{5}\)
\(S_{ABCD}=\dfrac{1}{2}AE.\left(AB+CD\right)=\dfrac{1}{2}.2\sqrt{5}.\left(2\sqrt{5}+10\right)=...\)

Câu 11.12.
Kẻ đường cao \(AH,BK\).
Do tam giác \(\Delta AHD=\Delta BKC\left(ch-gn\right)\)nên \(DH=BK\).
Đặt \(AB=AH=x\left(cm\right),x>0\).
Suy ra \(DH=\frac{10-x}{2}\left(cm\right)\)
Xét tam giác \(AHD\)vuông tại \(H\):
\(AD^2=AH^2+HD^2=x^2+\left(\frac{10-x}{2}\right)^2\)(định lí Pythagore)
Xét tam giác \(DAC\)vuông tại \(A\)đường cao \(AH\):
\(AD^2=DH.DC=10.\left(\frac{10-x}{2}\right)\)
Suy ra \(x^2+\left(\frac{10-x}{2}\right)^2=10.\frac{10-x}{2}\)
\(\Leftrightarrow x=2\sqrt{5}\)(vì \(x>0\))
Vậy đường cao của hình thang là \(2\sqrt{5}cm\).
Câu 11.11.
Kẻ \(AE\perp AC,E\in CD\).
Khi đó \(AE//BD,AB//DE\)nên \(ABDE\)là hình bình hành.
Suy ra \(AE=BD=15\left(cm\right)\).
Kẻ đường cao \(AH\perp CD\)suy ra \(AH=12\left(cm\right)\).
Xét tam giác \(AEC\)vuông tại \(A\)đường cao \(AH\):
\(\frac{1}{AH^2}=\frac{1}{AE^2}+\frac{1}{AC^2}\Leftrightarrow\frac{1}{AC^2}=\frac{1}{AH^2}-\frac{1}{AE^2}=\frac{1}{12^2}-\frac{1}{15^2}=\frac{1}{400}\)
\(\Rightarrow AC=20\left(cm\right)\)
\(S_{ABCD}=\frac{1}{2}AC.BD=\frac{1}{2}.15.20=150\left(cm^2\right)\),

Cách giải dạng toán này như sau: Ta thấy: 1/2 = 1 - 1/2
1/2 + 1/4 = 3/4 = 1- 1/4
1/2 + 1/4 + 1/8 = 7/8 = 1 - 1/8
Tương tự ta có:
1/2 + 1/4 +1/8 + 1/16 + 1/32 + 1/64 + 1/128 = 1 - 1/128 = 127/128.

Gọi a và b lần lượt là độ dài của đáy lớn và bé của hình thang \(\left(a>b>0\right)\)
Hình thang có diện tích là 140cm2
\(\Rightarrow8\left(a+b\right):2=140\) \(\Leftrightarrow a+b=35\) (1)
Mặt khác, độ dài 2 đáy hơn kém nhau 15cm \(\Rightarrow a-b=15\) (2)
Từ (1) và (2) \(\Rightarrow\left\{{}\begin{matrix}a=25\\b=10\end{matrix}\right.\left(TM\right)\)
Vậy độ dài đáy lớn và nhỏ lần lượt là 25cm và 10cm
Gọi đáy lớn và đáy nhỏ lần lượt là x và y (x>t; x>15)
Độ dài các đáy của hình thang hơn kém nhau 15cm nên ta có PT: x-y=15 (1)
Hình thang có diện tích 140cm2, chiều cao 8cm nên ta có PT:
\(\dfrac{8\left(x+y\right)}{2}=140\)
⇔x+y=35 (2)
Từ (1) và (2) ta có HPT: \(\left\{{}\begin{matrix}x-y=15\\x+y=35\end{matrix}\right.\)
Giải hệ ta được: \(\left\{{}\begin{matrix}x=25\\y=10\end{matrix}\right.\)
Vậy...

Câu 1: Tam giác ABC vuông tại A có AM là đường trung tuyến ứng với cạnh huyền BC
=> AM=\(\frac{1}{2}\)BC mà AM=6 cm=> BC=12cm.
Tam giác ANB vuông tại A có AN2+AB2=BN2 (Theo Pytago) mà BN=9cm (gt)
=>AN2+AB2=81 Lại có AN=\(\frac{1}{2}\)AC =>\(\frac{1}{2}\)AC2+AB2=81 (1)
Tam giác ABC vuông tại A có: AC2+AB2=BC2 => BC2 - AB2 = AC2 (2)
Từ (1) và (2) suy ra \(\frac{1}{4}\)* (BC2 - AB2)+AB2=81 mà BC=12(cmt)
=> 36 - \(\frac{1}{4}\)AB2+AB2=81
=> 36+\(\frac{3}{4}\)AB2=81
=> AB2=60=>AB=\(\sqrt{60}\)
C2
Cho hình thang cân ABCD có đáy lớn CD = 1
C4
Câu hỏi của Thiên An - Toán lớp 9 - Học toán với OnlineMath
Tổng độ dài đáy lớn và đáy nhỏ là:
105x2:6=35(m)
Độ dài đáy lớn là:
(35+5):2=20(m)
Độ dài đáy nhỏ là:
(35-5):2=15(m)
Đáp số:đáy lớn 20m
:đáy nhỏ 15m
Tổng hai đáy của hình thang là:
\(105.2:6=35\left(m\right)\)
Đáy lớn dài:
\(\left(35+5\right):2=20\left(m\right)\)
Đáy bé dài:
\(20-5=15\left(m\right)\)
Bài toán tổng hiệu lớp 4.