Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Thời điểm đầu tiên ứng với véc tơ quay từ M đến N
Góc quay: 600
Thời gian \(t=\frac{60}{360}T\)=\(\frac{1}{6}.\frac{2\pi}{100\pi}=\frac{1}{300}s\)

hình như bạn ấy viết thiếu Đặt điện áp u=310cos100pi*t(V) !

Đáp án B
Tại ![]() (biên dương) -> khoảng thời gian về
(biên dương) -> khoảng thời gian về 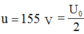 là
là
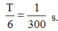 s. Chọn B.
s. Chọn B.

Đáp án C.
lúc đầu ta có :
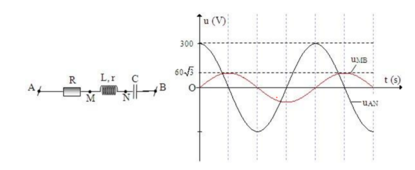
UMB=2UR => ZMB=2R <=> ZC=\(\sqrt{3}\)R mà C=\(\frac{L}{R^2}\) => ZL=\(\frac{R}{\sqrt{3}}\)
lúc sau ta có Uc' max :
Zc'.ZL=R2+ \(Z^2_L\) => Zc'=\(\frac{4R}{\sqrt{3}}\)
\(\text{tanφ}=\frac{Z_L-Z_C}{R}\Rightarrow\tan\varphi=-\sqrt{3}\Rightarrow\varphi=-\frac{\pi}{3}\)

Bài 1:
Trước hết có \(Z_L=Z_C=100\Omega\Rightarrow Z_m=100\sqrt{3}\Omega\Rightarrow I=\sqrt{\frac{7}{3}}A\)
suy ra \(U_{AN}=U_{BM}=200\sqrt{\frac{7}{3}}V\) ( sao số xấu thế?)
Vẽ giản đồ vecto dễ thấy $U_{AN}$ chậm pha hơn $U_{BM}$ một góc \(\frac{\pi}{3}\)
\(u_{AN}=200\sqrt{\frac{14}{3}}\cos\left(100\pi t+\varphi\right)=100\sqrt{3}\) \(\Rightarrow u_{BM}=200\sqrt{\frac{14}{3}}\cos\left(100\pi t+\varphi+\frac{\pi}{3}\right)\)
Mặt khác $U_{AN}$ đang tăng nên \(\sin\left(100\pi t+\varphi\right)< 0\) Từ đó áp dụng công thức khai triển $\cos$ suy ra \(u_{BM}=50\sqrt{3}+200\sqrt{\frac{989}{336}}\) (V)
Bài 2: Nối tắt 2 đầu điện trở?

Chọn D
Khi u L cực đại = 200 V.
u
R
trễ pha
π
2
so với
u
L
nên ![]()
![]()
Điện áp tức thời tại hai đầu đoạn mạch ![]() =150V
=150V
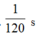
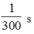
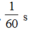
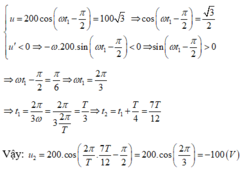

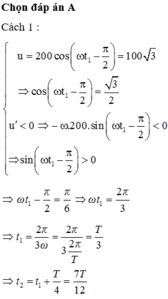

T=1/50
t=0 u=0 đang tăng
u=155=U0/ 2
t=T/12=1/600 --> C
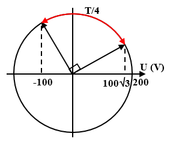
Biểu diễn điện áp bằng véc tơ quay.
Ban đầu, véc tơ tạo góc 900 hướng xuống. Sau đó nó quay 300 thì hình chiếu lên trục u có giá trị 155V.
Thời gian: \(t=\frac{30}{360}T=\frac{1}{12}.\frac{2\pi}{100\pi}=\frac{1}{600}s\)