Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a. Có \(8!\) cách xếp
b. Xếp 2 nữ cạnh nhau: có \(2!\) cách
Coi 2 nữ là 1 bạn, hoán vị với 6 nam, có \(7!\) cách
\(\Rightarrow\) Có \(8!-2!.7!\) cách xếp 2 nữ ko ngồi cạnh nhau
c. CHọn ra 4 em bất kì: \(C_8^4\) cách
Chọn 4 em không có nữ nào: \(C_6^4\) cách
Số cách thỏa mãn yêu cầu: \(C_8^4-C_6^4\)
d. Số cách chọn 3 em (có phân công thứ tự): \(A_8^3\) cách

Đáp án A
Số cách đi ra của 8 người bằng 13 8
Số cách đi ra của 8 người mà mỗi người một tầng bằng A 13 8
Xác suất cần tính bằng
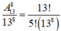

Số cách chọn thực đơn bữa ăn là:
Theo quy tắc nhân có 10. 5. 4 = 200 cách chọn

Đáp án C
Cách 1: Giải bằng hàm số
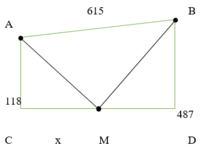
Đặt CM = x (x > 0)
Dễ tính ra CD ![]()
Từ đề bài ta có: f (x) = ![]()
Quãng đường ngắn nhất người đó có thể đi
⇔ Giá trị nhỏ nhất của f(x) trên (0;492)
Ta có: f’(x) = 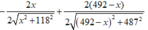
=> f’(x) = 0
![]()
![]()
![]()
![]()
![]()
Ta có bảng biến thiên
| x |
0 |
0 |
492 |
| y’ |
|
+ 0 - |
|
| y |
779,8 |
||
Vậy quãng đường ngắn nhất mà người đó có thể đi là: 779,8
Cách 2: Giải bằng hình học
Gọi B’ là điểm đối xứng của B qua D
Dễ thấy AM + MB = AM + MB’
⇔ AM + MB ngắn nhất
⇔ AM + MB’ ngắn nhất
Dễ thấy theo bất đẳng thức tam giác: AM + MB’ ≥ AB’
⇔ AM + MB’ ngắn nhất ó AM + MB’ = AB’
Dấu “=” xảy ra khi và chỉ khi A, M, B’ thẳng hàng
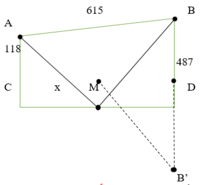

Đáp án B
Số cách đi từ tỉnh A đến tỉnh B là: C 4 1 = 4
Số cách đi từ tỉnh B đến tỉnh C là: C 3 1 = 3
Vậy số cách đi từ tỉnh A qua tỉnh B sau đó đến tỉnh C là: 4.3=12

Đáp án B
Các cách xác định mặt phẳng đúng: 2; 4 ; 8
1. Đi qua 3 điểm phân biệt không thẳng hàng
3. Trong trường hợp 2 đường thẳng chéo nhau thì không thể xác định được mặt phẳng
5. Song song với 2 đường thẳng cắt nhau Có vô số mặt phẳng như vậy.
Phương pháp xác định mặt phẳng chỉ đúng khi mặt phẳng này đi qua 1 điểm cho trước
6. Song song với 2 đường thẳng chéo nhau Có vô số mặt phẳng như vậy
Phương pháp xác định mặt phẳng chỉ đúng khi mặt phẳng này đi qua 1 điểm cho trước
7. Đi qua 1 điểm và song song với một đường thẳng cho trước. Có vô số mặt phẳng như vậy

Đáp án B.
Để đi vào có 4 cách chọn cửa và đi ra có 3 cách chọn cửa (Do đi ra là cửa khác cửa lúc đi vào )
Do đó theo quy tắc nhân có 4.3 = 12 cách đi vào và đi ra.