Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1.
ĐK: \(x\ne3;x\ne-2\)
\(\dfrac{5}{x-3}+\dfrac{3}{x+2}\le\dfrac{3+2x}{x^2-x-6}\)
\(\Leftrightarrow\dfrac{5\left(x+2\right)+3\left(x-3\right)}{x^2-x-6}\le\dfrac{3+2x}{x^2-x-6}\)
\(\Leftrightarrow\dfrac{8x+1-3-2x}{x^2-x-6}\le0\)
\(\Leftrightarrow\dfrac{6x-2}{x^2-x-6}\le0\)
\(\Leftrightarrow\left\{{}\begin{matrix}6x-2\ge0\\x^2-x-6< 0\end{matrix}\right.\) hoặc \(\left\{{}\begin{matrix}6x-2\le0\\x^2-x-6>0\end{matrix}\right.\)
TH1: \(\left\{{}\begin{matrix}6x-2\ge0\\x^2-x-6< 0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\ge\dfrac{1}{3}\\-2< x< 3\end{matrix}\right.\Leftrightarrow\dfrac{1}{3}\le x< 3\)
TH2: \(\left\{{}\begin{matrix}6x-2\le0\\x^2-x-6>0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\le\dfrac{1}{3}\\\left[{}\begin{matrix}x>3\\x< -2\end{matrix}\right.\end{matrix}\right.\Leftrightarrow x< -2\)
Vậy ...
2.
ĐK: \(x\ne\pm2\)
\(\dfrac{1}{x^2-4}+\dfrac{2}{x+2}>-\dfrac{3}{x-2}\)
\(\Leftrightarrow\dfrac{1}{x^2-4}+\dfrac{2\left(x-2\right)+3\left(x+2\right)}{x^2-4}>0\)
\(\Leftrightarrow\dfrac{5x+3}{x^2-4}>0\)
\(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}5x+3>0\\x^2-4>0\end{matrix}\right.\\\left\{{}\begin{matrix}5x+3< 0\\x^2-4< 0\end{matrix}\right.\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}-\dfrac{3}{5}< x< 2\\x< -2\end{matrix}\right.\)
Vậy ...

1.
\(x^4-6x^2-12x-8=0\)
\(\Leftrightarrow x^4-2x^2+1-4x^2-12x-9=0\)
\(\Leftrightarrow\left(x^2-1\right)^2=\left(2x+3\right)^2\)
\(\Leftrightarrow\left[{}\begin{matrix}x^2-1=2x+3\\x^2-1=-2x-3\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x^2-2x-4=0\\x^2+2x+2=0\end{matrix}\right.\)
\(\Leftrightarrow x=1\pm\sqrt{5}\)
3.
ĐK: \(x\ge-9\)
\(x^4-x^3-8x^2+9x-9+\left(x^2-x+1\right)\sqrt{x+9}=0\)
\(\Leftrightarrow\left(x^2-x+1\right)\left(\sqrt{x+9}+x^2-9\right)=0\)
\(\Leftrightarrow\sqrt{x+9}+x^2-9=0\left(1\right)\)
Đặt \(\sqrt{x+9}=t\left(t\ge0\right)\Rightarrow9=t^2-x\)
\(\left(1\right)\Leftrightarrow t+x^2+x-t^2=0\)
\(\Leftrightarrow\left(x+t\right)\left(x-t+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-t\\x=t-1\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-\sqrt{x+9}\\x=\sqrt{x+9}-1\end{matrix}\right.\)
\(\Leftrightarrow...\)

a) \(\left(x+1\right)\left(x-1\right)\left(3x-6\right)>0\)
Lập bảng xét dấu ta được kết quả :
\(Bpt\Leftrightarrow\left[{}\begin{matrix}-1< x< 1\\x>2\end{matrix}\right.\)
b) \(\dfrac{x+3}{x-2}\le0\)
Lập bảng xét dấu ta được kết quả :
\(Bpt\Leftrightarrow-3\le x< 2\)
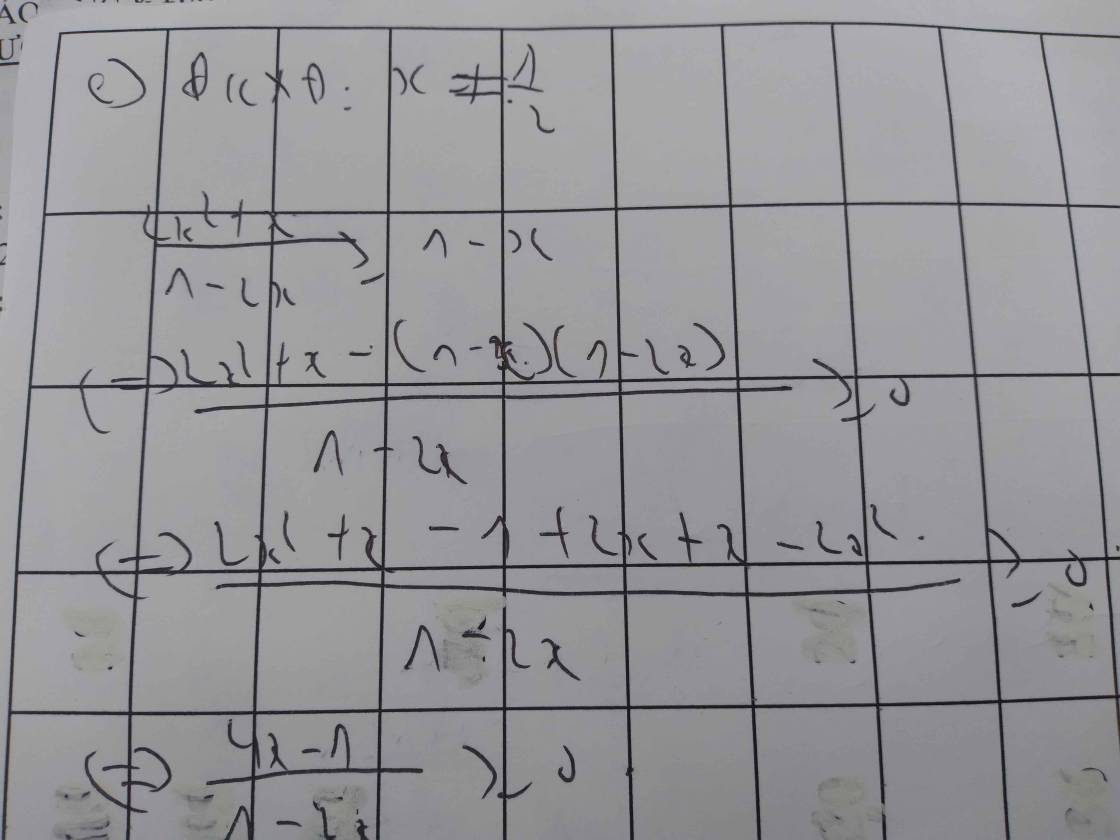
d) \(\dfrac{2x-5}{3x+2}< \dfrac{3x+2}{2x-5}\)
\(\Leftrightarrow\dfrac{2x-5}{3x+2}-\dfrac{3x+2}{2x-5}< 0\)
\(\Leftrightarrow\dfrac{\left(2x-5\right)^2-\left(3x+2\right)^2}{\left(3x+2\right)\left(2x-5\right)}< 0\)
\(\Leftrightarrow\dfrac{\left(2x-5+3x+2\right)\left(2x-5-3x-2\right)}{\left(3x+2\right)\left(2x-5\right)}< 0\)
\(\Leftrightarrow\dfrac{-\left(5x-3\right)\left(x+7\right)}{\left(3x+2\right)\left(2x-5\right)}< 0\)
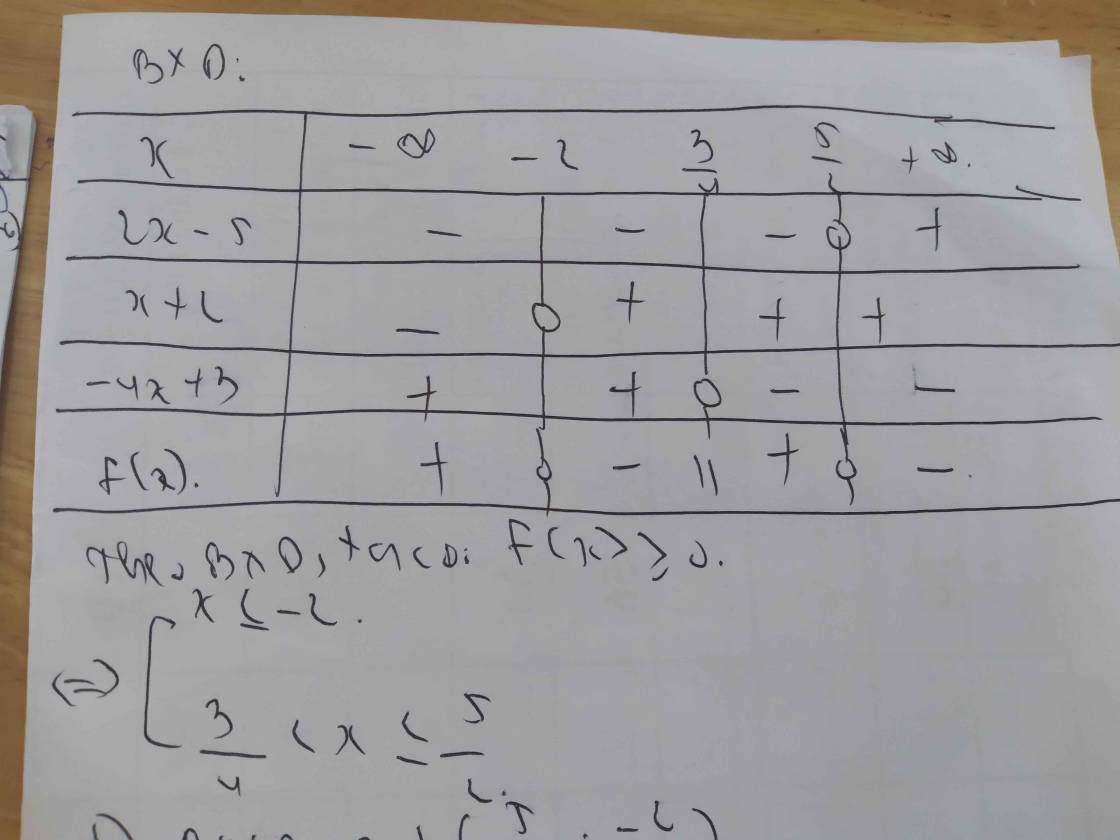
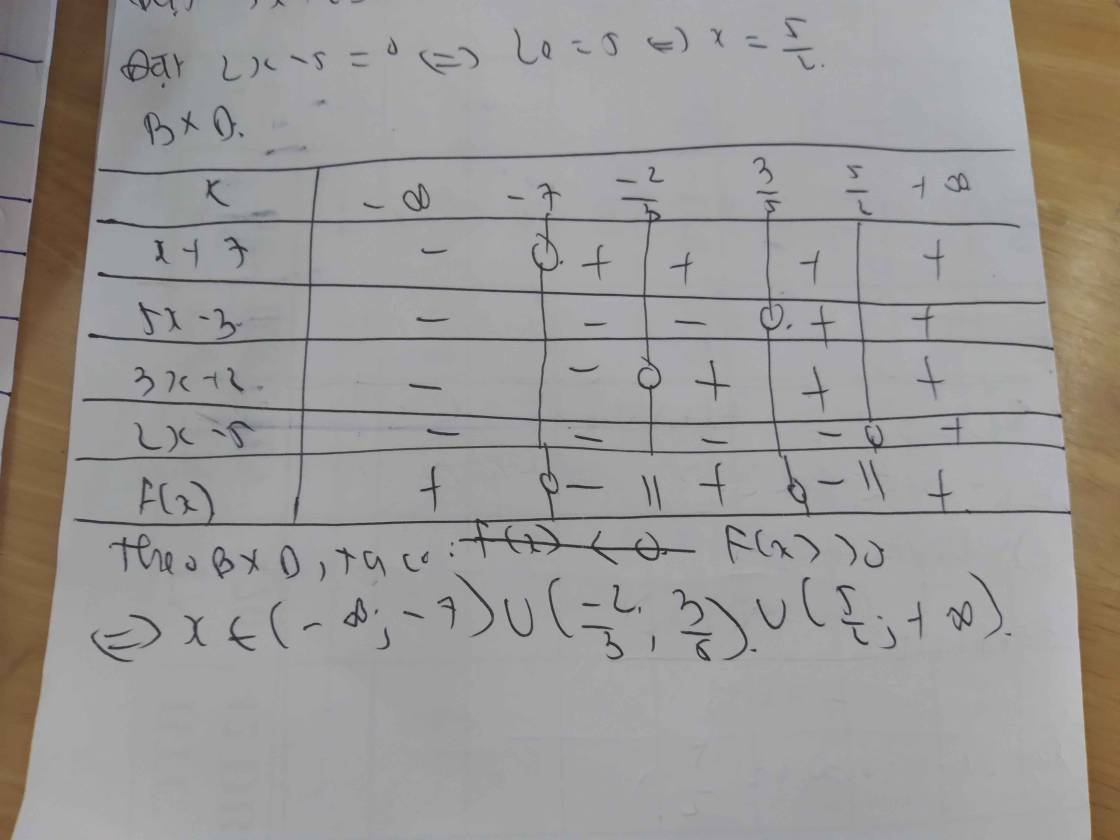
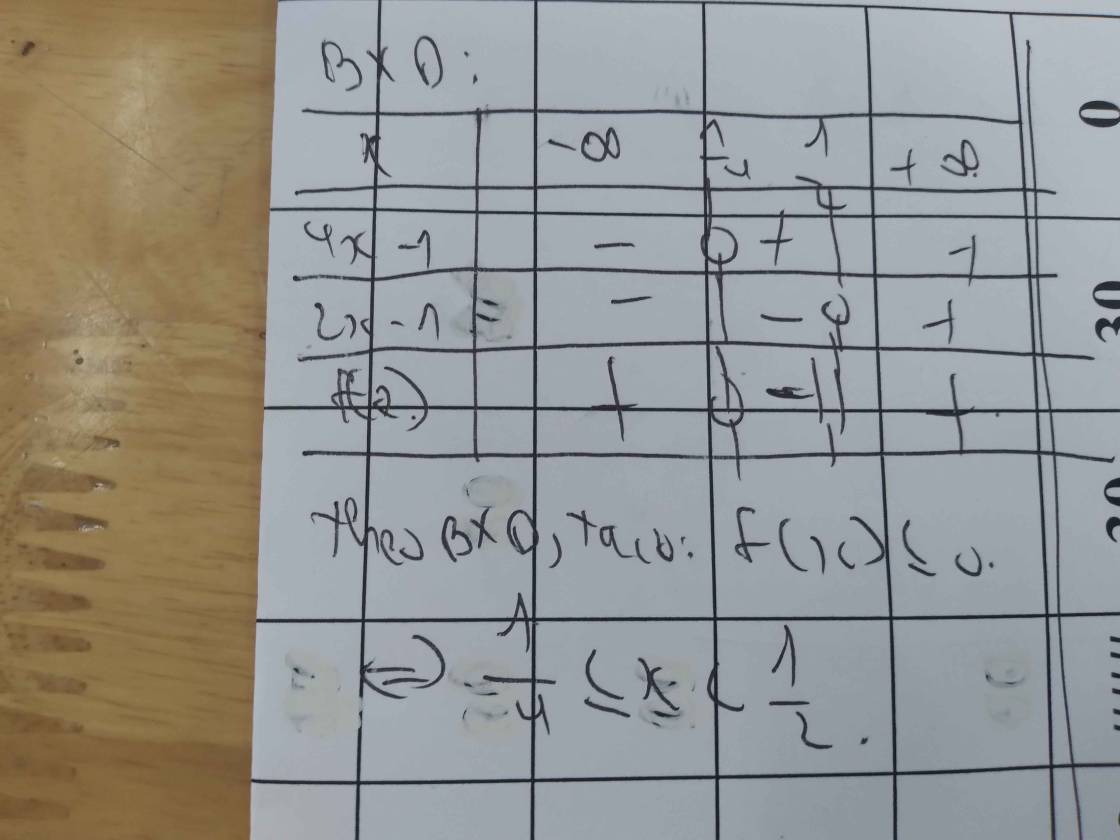
Lập bảng xét dấu ta được kết quả :
\(Bpt\Leftrightarrow\left[{}\begin{matrix}-7< x< -\dfrac{2}{3}\\\dfrac{5}{3}< x< \dfrac{5}{2}\end{matrix}\right.\)

4.
ĐK: \(x\ge0\)
Ta có \(1-\sqrt{2\left(x^2-x+1\right)}\le1-\sqrt{2}< 0\), khi đó:
\(\dfrac{x-\sqrt{x}}{1-\sqrt{2\left(x^2-x+1\right)}}\ge1\)
\(\Leftrightarrow x-\sqrt{x}\le1-\sqrt{2\left(x^2-x+1\right)}\)
\(\Leftrightarrow\sqrt{x}-\dfrac{1}{\sqrt{x}}-1+\sqrt{2\left(x+\dfrac{1}{x}-1\right)}\le0\)
\(\Leftrightarrow\sqrt{x}-\dfrac{1}{\sqrt{x}}-1+\sqrt{2\left(\sqrt{x}-\dfrac{1}{\sqrt{x}}\right)^2+2}\le0\)
\(\Leftrightarrow t-1+\sqrt{2t^2+2}\le0\left(t=\sqrt{x}-\dfrac{1}{\sqrt{x}}\right)\)
\(\Leftrightarrow\sqrt{2t^2+2}\le1-t\)
\(\Leftrightarrow\left\{{}\begin{matrix}1-t>0\\2t^2+2\le t^2-2t+1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}t< 1\\\left(t+1\right)^2\le0\end{matrix}\right.\)
\(\Leftrightarrow t=-1\)
\(\Leftrightarrow\sqrt{x}-\dfrac{1}{\sqrt{x}}+1=0\)
\(\Leftrightarrow x+\sqrt{x}-1=0\)
\(\Leftrightarrow x=\dfrac{3-\sqrt{5}}{2}\)

\(\dfrac{x-2}{x+1}-\dfrac{3}{x+2}>0.\left(x\ne-1;-2\right).\\ \Leftrightarrow\dfrac{x^2-4-3x-3}{\left(x+1\right)\left(x+2\right)}>0.\\ \Leftrightarrow\dfrac{x^2-3x-7}{\left(x+1\right)\left(x+2\right)}>0.\)
Đặt \(f\left(x\right)=\dfrac{x^2-3x-7}{\left(x+1\right)\left(x+2\right)}>0.\)
Ta có: \(x^2-3x-7=0.\Rightarrow\left[{}\begin{matrix}x=\dfrac{3+\sqrt{37}}{2}.\\x=\dfrac{3-\sqrt{37}}{2}.\end{matrix}\right.\)
\(x+1=0.\Leftrightarrow x=-1.\\ x+2=0.\Leftrightarrow x=-2.\)
Bảng xét dấu:
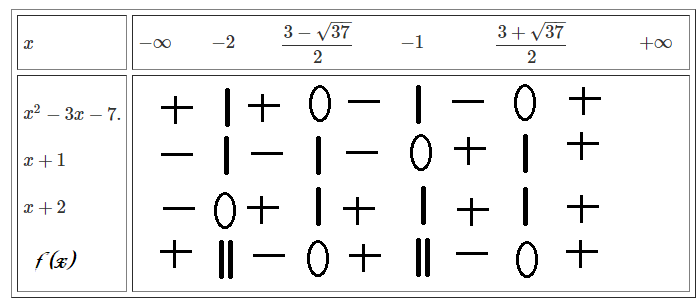
\(\Rightarrow f\left(x\right)>0\Leftrightarrow x\in\left(-\infty-2\right)\cup\left(\dfrac{3-\sqrt{37}}{2};-1\right)\cup\left(\dfrac{3+\sqrt{37}}{2};+\infty\right).\)
\(\sqrt{x^2-3x+2}\ge3.\\ \Leftrightarrow x^2-3x+2\ge9.\\ \Leftrightarrow x^2-3x-7\ge0.\)
\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{3-\sqrt{37}}{2}.\\x=\dfrac{3+\sqrt{37}}{2}.\end{matrix}\right.\)
Đặt \(f\left(x\right)=x^2-3x-7.\)
\(f\left(x\right)=x^2-3x-7.\)
\(\Rightarrow f\left(x\right)\ge0\Leftrightarrow x\in(-\infty;\dfrac{3-\sqrt{37}}{2}]\cup[\dfrac{3+\sqrt{37}}{2};+\infty).\)
\(\Rightarrow\sqrt{x^2-3x+2}\ge3\Leftrightarrow x\in(-\infty;\dfrac{3-\sqrt{37}}{2}]\cup[\dfrac{3+\sqrt{37}}{2};+\infty).\)





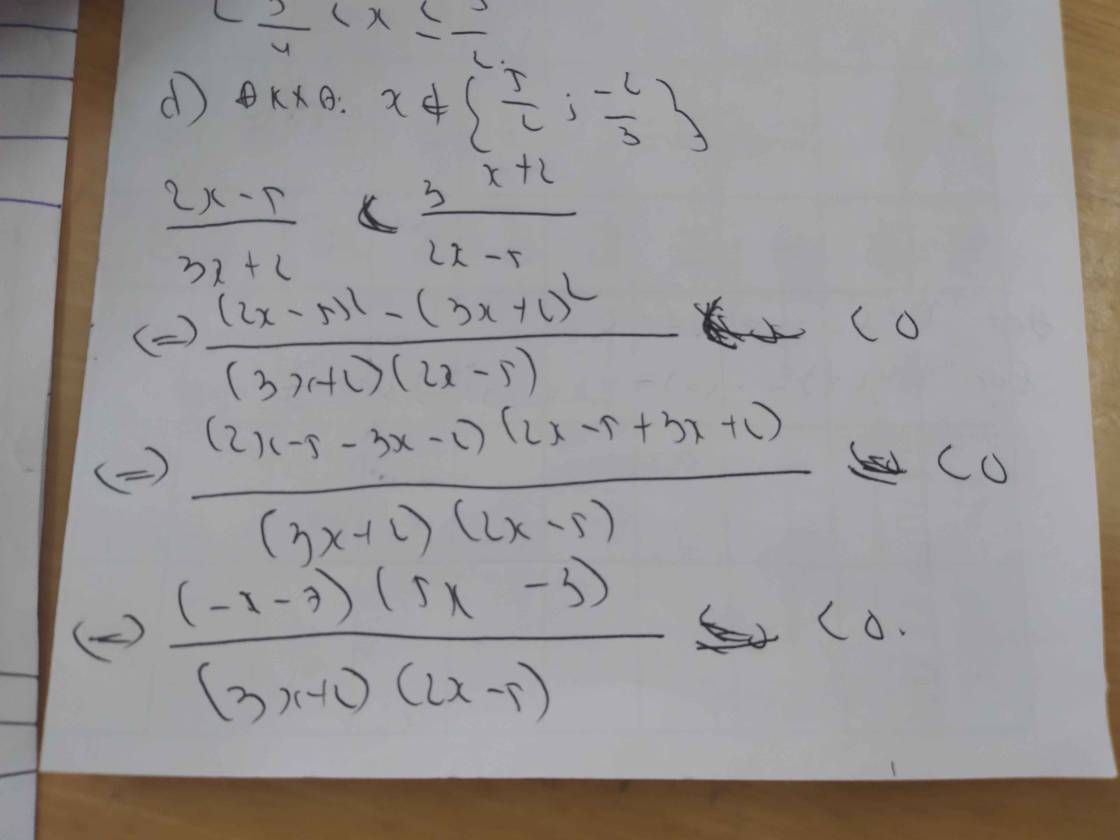


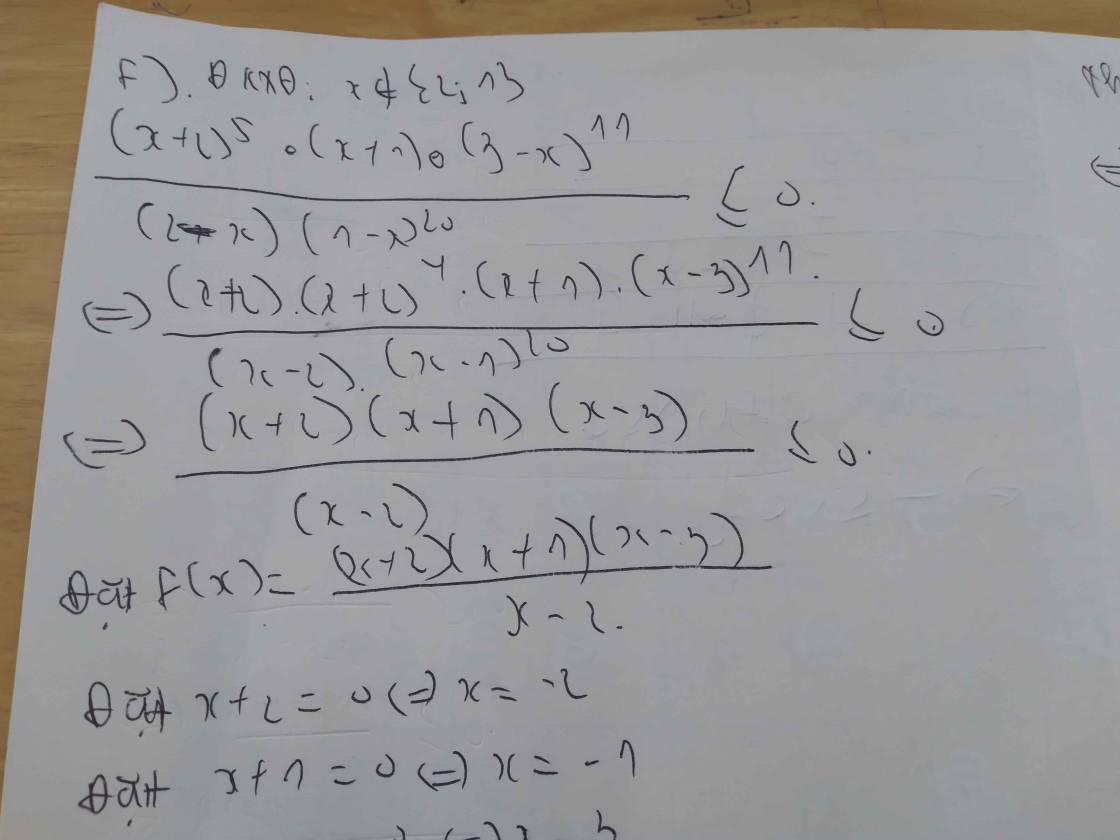


ĐK \(x\ne-2;-3;-5;-6\)
\(\Leftrightarrow\dfrac{x-1}{x+2}-1-\left(\dfrac{x-2}{x+3}-1\right)=\dfrac{x-4}{x+5}-1-\left(\dfrac{x-5}{x+6}-1\right)\)
\(\Leftrightarrow\dfrac{x-1-x-2}{x+2}-\dfrac{x-2-x-3}{x+3}=\dfrac{x-4-x-5}{x+5}-\dfrac{x-5-x-6}{x+6}\)
\(\Leftrightarrow\dfrac{-3}{x+2}-\dfrac{-5}{x+3}=\dfrac{-9}{x+5}-\dfrac{-11}{x+6}\)
\(\Leftrightarrow\dfrac{3}{x+2}-\dfrac{5}{x+3}=\dfrac{9}{x+5}-\dfrac{11}{x+6}\)
\(\Leftrightarrow\dfrac{3}{x+2}+\dfrac{11}{x+6}=\dfrac{9}{x+5}+\dfrac{5}{x+3}\)
\(\Leftrightarrow\dfrac{3\left(x+6\right)+11\left(x+2\right)}{\left(x+2\right)\left(x+6\right)}=\dfrac{9\left(x+3\right)+5\left(x+5\right)}{\left(x+3\right)\left(x+5\right)}\)
\(\Leftrightarrow\dfrac{14x+40}{\left(x+2\right)\left(x+6\right)}=\dfrac{14x+52}{\left(x+3\right)\left(x+5\right)}\)
\(\Leftrightarrow\left(x+2\right)\left(x+6\right)\left(14x+52\right)=\left(x+3\right)\left(x+5\right)\left(14x+40\right)\)
\(\Leftrightarrow\left(x^2+8x+12\right)\left(14x+52\right)=\left(x^2+8x+15\right)\left(14x+40\right)\)
\(\Leftrightarrow14x\left(x^2+8x+12\right)+52\left(x^2+8x+12\right)=14x\left(x^2+8x+15\right)+40\left(x^2+8x+15\right)\)
\(\Leftrightarrow14x\left(x^2+8x\right)+12.14x+52\left(x^2+8x\right)+52.12=14x\left(x^2+8x\right)+15.14x+40\left(x^2+8x\right)+15.40\)
\(\Leftrightarrow12\left(x^2+8x\right)-42x+24=0\)
\(\Leftrightarrow12x^2+54x+24=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{1}{2}\\x=-4\end{matrix}\right.\)