Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Câu 1
a.
Xét \(\Delta ABC\) có :
\(\widehat{ABC}+\widehat{BAC}+\widehat{BCA}=180^o\) ( định lý tổng 3 góc của 1 \(\Delta\) )
\(\Rightarrow\widehat{BCA}=40^o\) (1)
Ta có Ax là tia đối của AB
suy ra \(\widehat{BAC}+\widehat{CAx}=180^o\)
\(\widehat{CAx}=80^o\)
lại có Ay là tia phân giác \(\widehat{CAx}\)
\(\Rightarrow\widehat{xAy}=\widehat{yAc}=\dfrac{\widehat{CAx}}{2}=\dfrac{80^o}{2}=40^o\) (2)
Từ (1)(2) suy ra \(\widehat{yAc}=\widehat{ACB}=40^o\)
mà chúng ở vị trí so le trong
\(\Rightarrow\) Ay//BC
Bài 2
Rảnh làm sau , đến giờ học rồi .

Bài làm
a) Xét ∆ABC vuông tại B có:
^BAC + ^C = 90°
Hay ^BAC + 30° = 90°
=> ^BAC = 60°
Vì AD là phân giác của góc BAC.
=> ^DAC = 60°/2 = 30°
Xét tam giác ADC có:
^DAC + ^ACD + ^ADC = 180°
Hay 30° + 30° + ^ADC = 180°
=> ^ADC = 180° - 30° - 30°
=> ^ADC = 120°
b) Xét tam giác ABD và tam giác AED có:
AB = AE ( gt )
^BAD = ^EAD ( Do AD phân giác )
Cạnh AD chung.
=> ∆ABD = ∆AED ( c.g.c )
c) Vì ∆ABD = ∆AED ( cmt )
=> ^ABD = ^AED = 90°
=> DE vuông góc với AC tại E (1)
Ta có: ^DAC = ^DCA = 30°
=> ∆DAC cân tại D.
=> AD = DC
Xét tam giác DEA và tam giác DEC có:
Góc vuông: ^DEA = ^DEC ( = 90° )
Cạnh huyền AD = DC ( cmt )
Góc nhọn: ^DAC = ^DCA ( cmt )
=> ∆DEA = ∆DEC ( g.c.g )
=> AE = EC
=> E là trung điểm của AC. (2)
Từ (1) và (2) => DE là trung trực của AC ( đpcm )

,chú tuổi gì, Thiên Thảo, Guyo, Mai Linh,Phạm Thái Dương, Lưu Thùy Dung, Nguyễn Văn Toàn, Hoa Thiên Lý, Sky SơnTùng, Nguyễn Thái Bình, Akai Haruma, Nhã Doanh, Phạm Nguyễn Tất Đạt, ngonhuminh, Mashiro Shiina, Nguyễn Minh Hùng, Nguyễn Thanh Hằng, nguyen thi vang, Phùng Khánh Linh, kuroba kaito, Nguyễn Huy Tú, Hoàng Lê Bảo Ngọc, Trần Việt Linh, Võ Đông Anh Tuấn, Phương An, soyeon_Tiểubàng giải, Ace Legona, ...

Trên cạnh BA của \(\Delta\)ABC lấy điểm G sao cho BG = BC. Ta có:
^CFB = 1800 - ^BCF - ^CBF = 1800 - ^BCE - ^CBE = 700 => ^CFB = ^BCF (=700)
=> \(\Delta\)CBF cân tại B => BF = BC = BG => \(\Delta\)GBF cân tại B => ^BGF = (1800 - ^GBF)/2 = 800
=> ^FGA = 1000. Gọi GF cắt AC tại L. Trên đoạn GL lấy điểm F' sao cho ^CAF' = 100
Qua F' dựng đường thẳng song song với AB, đường thẳng này cắt AC tại H
Trên nửa mặt phẳng bờ AB có chứa điểm C, dựng \(\Delta\)GAK đều
Xét \(\Delta\)ALG: ^LGA = 1000 (cmt), ^LAG = 400 => \(\Delta\)ALG cân tại G => \(\Delta\)LF'H cân tại F' (F'H // AG)
Xét \(\Delta\)CLG: ^GCL = ^ACB - ^BCG = 200, ^CLG = 1800 - ^GLA = 1400 => \(\Delta\)CLG cân tại L
Có ^GAF' = ^BAC - ^CAF' = 300 = ^GAK/2 => ^GAF' = ^KAF'. Từ đây dễ có \(\Delta\)F'GA = \(\Delta\)F'KA (c.g.c)
=> F'G = F'K => \(\Delta\)GF'K cân tại F'. Do ^F'GK = ^F'GA - ^KGA = 400 nên ^GF'K = 1000
Suy ra ^GF'K = ^HF'L (= ^AGL = 1000) => ^GF'H = ^KF'L (= 1000 - ^KF'H)
Kết hợp với F'H = F'L; F'G = F'K (cmt) suy ra \(\Delta\)HF'G = \(\Delta\)LF'K (c.g.c) => ^F'LK = ^F'HG
Dễ dàng tính được ^F'LK = ^GLK = (1800 - 400)/2 = 700 => ^F'HG = 700 => ^HGA = 700 (Vì F'H // AG)
Ta thấy \(\Delta\)AGH có ^GAH = 400 , ^HGA = 700 => \(\Delta\)AGH cân tại A
Từ đó AH = AG = GL = CL (Vì các tam giác AGL, CLG cân). Dễ dàng chứng minh:
\(\Delta\)CLF' = \(\Delta\)AHF' (c.g.c) (F'L = F'H, ^F'LC = ^F'HA, CL = AH) => ^LCF' = ^HAF' = ^CAF' = 100
=> ^BCF' = 700 = ^BCE => CF' trùng CE. Ban đầu ta nhận thấy CE cắt GL tại F
Mà CF' trùng CE, F' thuộc GL nên F' trùng F. Tức là ^CAF = ^CAF' = 100 => ^CAF + ACB = 900
Vậy thì AF vuông góc với BC (đpcm).
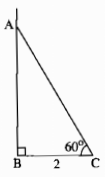
Xét ΔABC có \(\cos B=\dfrac{BA^2+BC^2-AC^2}{2\cdot BA\cdot BC}=\dfrac{16^2-14^2+BC^2}{2\cdot16\cdot BC}\)
\(\Leftrightarrow\dfrac{BC^2+60}{32BC}=\dfrac{1}{2}\)
\(\Leftrightarrow2BC^2-32BC+60=0\)
\(\Leftrightarrow BC^2-16BC+30=0\)
\(\Leftrightarrow BC^2-16BC+64-34=0\)
\(\Leftrightarrow\left[{}\begin{matrix}BC-8=\sqrt{34}\\BC-8=-\sqrt{34}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}BC=\sqrt{34}+8\left(cm\right)\\BC=-\sqrt{34}+8\left(cm\right)\end{matrix}\right.\)