Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
Đặt t = 4 x > 0 ⇒ m + 1 t 2 − 2 2 m − 3 + 6 m + 5 = 0
ĐK để PT có 2 nghiệm là: 2 m − 3 m + 1 > 0 6 m + 5 m + 1 > 0 Δ ' = 2 m − 3 2 − m + 1 6 m + 5 *
Khi đó: 4 x 1 = t 1 ; 4 x 2 = t 2 ⇒ x 1 x 2 = log 4 t 1 . log 4 t 2 < 0 ⇔ 0 < t 1 < 1 < t 2
⇔ t 1 − 1 t 2 − 1 < 0 ⇔ t 1 t 2 − t 1 − t 2 + 1 < 0 ⇔ 6 m + 5 m + 1 − 2 2 m − 3 m + 1 + 1 < 0 ⇔ 3 m + 12 m + 1 < 0 ⇔ − 1 < m < − 4
Kết hợp (*) ⇒ m = − 2 ; m = − 3.

Đáp án C
PT ⇔ m x 2 + 2 x 3 − 2 x 2 + 2 x + 2 = 0
→ t = x 2 + 2 x m t 3 − 2 t + 2 = 0 1 .
Ta có: f x = x 2 + 2 x , x ≤ − 3 ⇒ f x ≥ 3 ⇒ t ∈ 3 ; + ∞
1 ⇔ m = 2 t 2 − 2 t 3 = f t với t ∈ 3 ; + ∞ .
Ta có: f ' t = − 4 t 3 + 6 t 4 ⇒ f ' t = 0 ⇔ t = 3 2 ⇒ f t
nghịch biến trên 3 ; + ∞ ⇒ f 3 ; + ∞ t ≤ f 3 = − 2 27
Suy ra m ≤ − 2 27 ⇒ Có vô số giá trị của m.

Chọn B.
Phương pháp:
Đưa phương trình về dạng tích, giải phương trình tìm nghiệm và tìm điều kiện để bài toán thỏa.
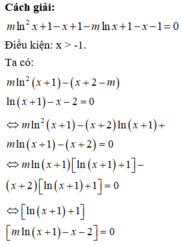
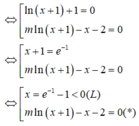

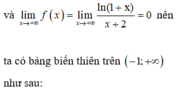


Đáp án A
Phương pháp: Chia cả 2 vế cho 3x, đặt  , tìm điều kiện của t.
, tìm điều kiện của t.
Đưa về bất phương trình dạng ![]()
Cách giải :
![]()

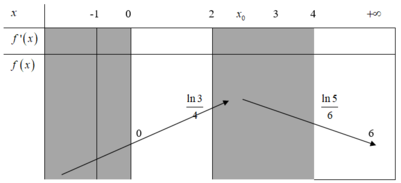
Ta có 

Đặt  , khi đó phương trình trở thành
, khi đó phương trình trở thành
![]()

![]()
![]()
![]()
![]()
Ta có: 



Vậy 
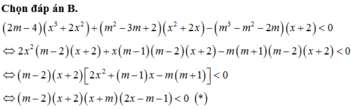


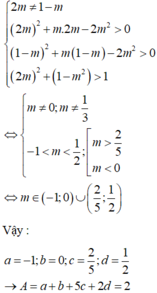
Đáp án D