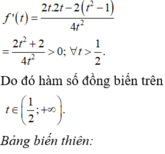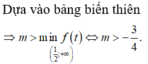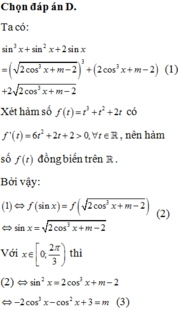Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án A
Phương pháp: Chia cả 2 vế cho 3x, đặt 
, tìm điều kiện của t.
Đưa về bất phương trình dạng 
Cách giải :
Ta có 
Đặt 
, khi đó phương trình trở thành
Ta có: 
Vậy 
Đáp án C
log 2 2 2 x − 2 m + 1 log 2 x − 2 < 0 ⇔ 1 + log 2 x 2 − 2 m + 1 log 2 x − 2 < 0
Đặt t = log 2 x ta được 1 + t 2 − 2 m + 1 t − 2 < 0 ⇔ t 2 − 2 m t − 1 < 0 ⇔ t ∈ m − m 2 + 1 ; m + m 2 + 1
x ∈ 2 ; + ∞ ⇔ t ∈ 1 2 ; + ∞
⇒ m + m 2 + 1 > 1 2 ⇔ m > − 3 4
Đáp án B
Phương pháp:
- Biến đổi phương trình về phương trình bậc hai đối với log 2 x − 2 và đặt ẩn phụ t = log 2 x − 2 với t ∈ − 1 ; 1
- Rút m theo t và xét hàm f(t) để tìm ra điều kiện của m.
Cách giải:
m − 1 log 1 2 2 x − 2 2 + 4 m − 5 log 1 2 1 x − 2 + 4 m − 4 = 0 x > 2
m − 1 log 2 2 x − 2 + m − 5 log 2 x − 2 + m + 1 = 0
Đặt y = log 2 x − 2 ⇒ x ∈ 5 2 ; 4 ⇒ t ∈ − 1 ; 1
Phương trình đã cho trở thành:
m − 1 t 2 + m − 5 t + m + 1 = 0
⇔ m t 2 + t + 1 = t 2 + 5 t + 1 ⇔ m = t 2 + 5 t + 1 t 2 + t + 1 = 1 + 4 t t 2 + t + 1
vì t 2 + t + 1 > 0 ∀ t ∈ − 1 ; 1
Xét hàm số: y = 1 + 4 t t 2 + t + 1 trên − 1 ; 1
Có: y ' t = − 4 t 2 + 4 t 2 + t + 1 2
y ' x = 0 ⇔ − 4 t 2 + 4 t 2 + t + 1 2 = 0 ⇔ t = ± 1 ∈ − 1 ; 1
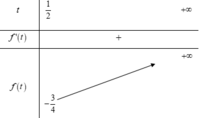
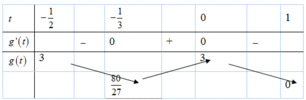
Ta có bảng biến thiên:
⇒ m ∈ − 3 ; 7 3 ⇒ a + b = − 2 3 .
Chú ý khi giải: HS thường nhầm lẫn các công thức biến đổi logarit dẫn đến kết quả sai, hoặc nhầm lẫn trong bước xét hàm f(t) để đi đến kết luận.
Đáp án B.
Với x ∈ 5 2 ; 4 thì phương trình tương đương với:
m - 1 log x 2 x - 2 + m - 5 log 2 x - 2 + m - 1 = 0 (1)
Đặt log 2 x - 2 = t . Với x ∈ 5 2 ; 4 thì t ∈ - 1 ; 1 . Phương trình (1) trở thành:
m - 1 t 2 + m - 5 + m - 1 = 0 ⇔ m t 2 + t + 1 = t 2 + 5 t + 1 ⇔ m = t 2 + 5 t + 1 t 2 + t + 1 (2)
Xét hàm số f ( t ) = t 2 + 5 t + 1 t 2 + t + 1 = 1 + 4 t t 2 + t + 1 trên đoạn - 1 ; 1 .
Đạo hàm f ' ( t ) = - 4 t 2 - 1 t 2 + t + 1 2 ≥ 0 , ∀ t ∈ - 1 ; 1 ; f ' ( t ) = 0 ⇔ t = ± 1 . Khi đó hàm số [-1;1] đồng biến trên [-1;1]. Suy ra m i n [ - 1 ; 1 ] f ( t ) = f ( - 1 ) = - 3 m a x [ - 1 ; 1 ] f ( t ) = f ( 1 ) = 7 3 .
Phương trình (2) có nghiệm ⇔ Đường thẳng y - m cắt đồ thị hàm số
f ( t ) ⇔ - 3 ≤ m ≤ 7 3 . Vậy S = - 3 ; 7 3 → a = - 3 b , b = 7 3 → a = - 3 , b = 7 3 → a + b = - 3 + 7 3 = - 2 3 .