
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 1
1, Ta có \(A=\frac{10}{56}+\frac{10}{140}+\frac{10}{260}+....+\frac{10}{1400}\)
\(A=\frac{5}{28}+\frac{5}{70}+\frac{5}{130}+...+\frac{5}{700}\)
\(A=\frac{5}{4.7}+\frac{5}{7.10}+\frac{5}{10.13}+....+\frac{5}{25.28}\)
\(A=5.\left(\frac{1}{4.7}+\frac{1}{7.10}+\frac{1}{10.13}+....+\frac{1}{25.28}\right)\)
\(A=5.\left(\frac{1}{4}-\frac{1}{7}+\frac{1}{7}-\frac{1}{10}+\frac{1}{10}-\frac{1}{13}+...+\frac{1}{25}-\frac{1}{28}\right)\)
\(A=5.\left(\frac{1}{4}-\frac{1}{28}\right)=5.\frac{3}{14}=\frac{15}{14}\)
Vậy \(A=\frac{15}{14}\)
2,
a) \(A=\frac{2n-7}{n-5}=\frac{2n-7-3+3}{n-5}=\frac{\left(2n-10\right)+3}{n-5}=\frac{3}{n-5}\)
Suy ra để A có giá trị nguyên thì \(n-5\inƯ\left(3\right)\)
Mà \(Ư\left(3\right)=\left\{1;-1;3;-3\right\}\)
Khi đó \(n-5\in\left\{1;-1;3;-3\right\}\)
Suy ra \(n\in\left\{6;4;8;2\right\}\)
Vậy ......
b) Ta có : \(A=\frac{2n-7}{n-5}=\frac{2n-7-3+3}{n-5}=\frac{\left(2n-10\right)+3}{n-5}=2+\frac{3}{n-5}\)
Để A có giá trị lớn nhất \(\Leftrightarrow\frac{2n-7}{n-5}\)lớn nhất \(\Leftrightarrow2+\frac{3}{n-5}\)lớn nhất \(\Leftrightarrow\frac{3}{n-5}\)lớn nhất \(\Leftrightarrow n=6\)
Khi đó A = 5
Vậy A đạt GTLN khi và chỉ khi n = 6

Ta có:
\(2n:\left(1+\frac{1}{1+2}+\frac{1}{1+2+3}+.....+\frac{1}{1+2+...+n}\right)=2020\)
<=> \(2n:\left(\frac{2}{2}+\frac{2}{3.2}+\frac{2}{4.3}+...+\frac{2}{\left(n+1\right).n}\right)=2020\)
<=> \(n:\left(1+\frac{1}{2.3}+\frac{1}{3.4}+...+\frac{1}{n\left(n+1\right)}\right)=2020\)
<=> \(n:\left(1+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+...+\frac{1}{n}-\frac{1}{n+1}\right)=2020\)
<=> \(n:\left(1-\frac{1}{n+1}\right)=2020\)
<=> \(n:\frac{n}{n+1}=2020\)
<=> n + 1 = 2020
<=> n = 2019


Để \(\frac{2n+1}{n+1}\)là số nguyên thì \(2n+1⋮n+1\)
Mà \(2\left(n+1\right)⋮n+1\)hay \(2n+2⋮n+1\)
\(\Rightarrow\left(2n+2\right)-\left(2n+1\right)⋮n+1\)
\(\left(2n-2n\right)+\left(2-1\right)⋮n+1\)
\(2⋮n+1\)
\(\Rightarrow n+1\inƯ\left(2\right)\)
\(\Rightarrow n+1\in\left\{1;2;-1;-2\right\}\)
\(\Rightarrow n\in\left\{0;1;-2;-3\right\}\)(TM)
HT
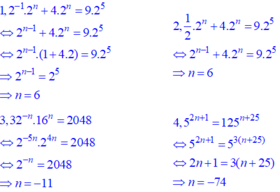
Ta có: \(\frac{1}{2}.2^n+4.2^n=9.2^5\)
\(\Rightarrow2^n.\left(\frac{1}{2}+4\right)=288\)
\(\Rightarrow2^n.\frac{9}{2}=288\)
\(\Rightarrow2^n=288:\frac{9}{2}=64\)
Mà \(64=2^6\)
Nên \(2^n=2^6\)
=> n = 6
Vậy n = 6
2^n+4.2^n=288:1/2=576
2^n(1+4)=576
2^nx5=576
bạn tự làm nốt