Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chiều rộng hình chữ nhật là :
15 + 25 =40 (cm)
Chiều dài hình chữ nhật hay độ dài đáy của hình tam giác là :
2400:40 = 60 (cm)
Diện tích hình tam giác MDC là :
25 * 60:2=750 (cm2)
Đáp số : 750 cm2

Tỉ số diện tích của hình chữ nhật IOND và OKCN là: 36 : 9 = 4 (lần).
- Hình chữ nhật IOND và OKCN có chung cạnh ON do đó IO = OK x 4.
- Hình chữ nhật AMOI và MBKO có chung cạnh MO, mà độ dài cạnh IO = OK x 4. Do đó diện tích hình chữ nhật AMOI bằng 4 lần diện tích hình chữ nhật MBKO.
- Diện tích hình chữ nhật AMOI là: 18 x 4 = 72 (cm2).
- Diện tích hình chữ nhật ABCD là: 72 + 18 + 9 + 36 = 135 (cm2).
b) (2,5 điểm). Diện tích hình tam giác MOI là: 72 : 2 = 36 (cm2).
Diện tích hình tam giác MOK là: 18 : 2 = 9 (cm2). (0,5đ) Diện tích hình tam giác OKN là: 9 : 2 = 4,5 (cm2).
Diện tích hình tam giác OIN là: 36 : 2 = 18 (cm2).
Diện tích hình tứ giác MKNI là: 36 + 9 + 4,5 + 18 = 67,5 (cm2).

Câu 5:
a) Số học sinh nữ của trường Tiểu học đó là:
\(40\%\times850=340\left(hs\right)\)
b) Số học sinh nam của trường Tiểu học là:
\(850-340=510\left(hs\right)\)
Tỉ số phần trăm giữ số học sinh nữ và số học sinh nam là:
\(\left(340\times100\%\right):510=66,67\%\)
Đáp số: ...

Giải
A B C D N
Vì ABCD là hình chữ nhật nên \(AB=CD=40cm\)
Mà BN = NA nên N là trung điểm của AB hay BN = NA \(=\frac{AB}{2}=\frac{40}{2}=20cm\)
Theo đề bài , ta có : \(\frac{NB.BC}{2}=180cm^2\)
\(\Leftrightarrow NB.BC=180cm^2.2\)
\(\Leftrightarrow20.BC=360cm^2\)
\(\Leftrightarrow BC=\frac{360cm^2}{20}\)
\(\Leftrightarrow BC=18cm^2\)
\(\Rightarrow S_{ABCD}=40.18=720\left(cm^2\right)\)
Vậy diện tích hình thang ANCD là :
\(720-180=540\left(cm^2\right)\)
Đáp số : 540 cm2

Bài 221:
Bán kính hình tròn là:
$12,56:2:3,14=2$ (cm)
Diện tích hình tròn là:
$2\times 2\times 3,14=12,56$ (cm2)
Bài 219:
a. Bán kính: $15:2=7,5$ (cm)
Diện tích hình tròn: $7,5\times 7,5\times 3,14=176,625$ (cm2)
b. Bán kính: $0,2:2=0,1$ (m)
Diện tích hình tròn: $0,1\times 0,1\times 3,14=0,0314$ (m2)
c. Bán kính: $\frac{2}{5}:2=0,2$ (dm)
Diện tích hình tròn: $0,2\times 0,2\times 3,14=0,1256$ (dm2)
ABCD là hình chữ nhật. BN=NA. Tính diện tích hình thang ANCD. Biết DC=40m và diện tích BNC là 180 m2

hi vẽ tranh, sáng tác thơ, truyện về an toàn giao thông.
CHƯƠNG TRÌNH THI VẼ TRANH, SÁNG TÁC THƠ,
TRUYỆN VỀ AN TOÀN GIAO THÔNG
(Lớp 5B, Trường Tiểu học Lê Hồng Phong)
I. Mục đích
– Tuyên truyền, vận động học sinh chấp hành tốt Luật an toàn giao thông.
– Phát hiện tài năng nghệ thuật của học sinh.
– Động viên học sinh tham gia hoạt động tập thể.
II. Phân công chuẩn bị
– Ban giám khảo: Giáo viên chủ nhiệm, lớp trưởng, lớp phó Văn – Thế – Mĩ.
– Phổ biến nội dung, kế hoạch thi: Lớp trưởng.
– Chuẩn bị quà thưởng: Giáo viên chủ nhiệm, ban chấp hành chi hội phụ huynh của lớp.
III. Chương trình cụ thể
– Họp lớp phổ biến nội dung thi: Tiết sinh hoạt lớp trưa thứ sáu ngày 5/ 4/2013.
– Nộp bài dự thi ngày 18/4/2013 cho các tổ trướng.
– Chấm thi ngày 20/4/2013.
Tổng kết phát thưởng ngày 22/4/2013.
Bài giải
Đoạn thẳng BN dài số m là:
40:2=20(m)
Đoạn thẳng BD dài số m là:
180x2:20=18(m)
Diện tích hình thang ANCD là:
(20+40)x18:2=540(m2)
Đ/s:540m2
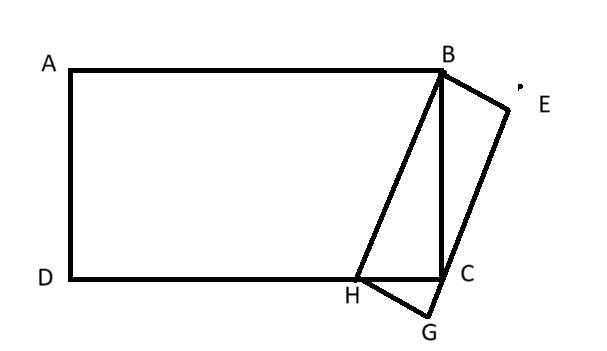









A B C D E G H K
Hạ \(CK\perp BH\) tại K
\(S_{BCH}=\dfrac{1}{2}xBHxCK\)
\(S_{BEGH}=BHxGH=BHxCK\)
\(\Rightarrow S_{BCE}+S_{CHG}=S_{BEGH}-S_{BCH}=\dfrac{1}{2}xBHxCK=S_{BCH}\)
Ta có
\(HC=\dfrac{1}{4}DC\Rightarrow DC=4xHC\)
\(S_{BCH}=\dfrac{1}{2}xBCxHC\)
\(S_{ABCD}=BCxDC=BCx4xHC\)
\(\Rightarrow\dfrac{S_{BHC}}{S_{ABCD}}=\dfrac{1}{8}\Rightarrow S_{ABCD}=8xS_{BCH}\)
Ta có
\(S_{ABEGHD}=S_{ABCD}+S_{BCE}+S_{CHG}=8xS_{BCH}+S_{BCH}=9xS_{BCH}=180cm^2\)
\(\Rightarrow S_{BCH}=180:9=20cm^2\)
\(\Rightarrow S_{ABCD}=8xS_{BCH}=8x20=160cm^2\)
\(S_{BEGH}=S_{BCH}+S_{BCE}+S_{CHG}=2xS_{BCH}=2x20=40cm^2\)