Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

bạn làm chính xác rùi
ôi thần linh ơi
bài này mình giải sai rùi,mai phải nộp cho thầy cám ơn nhé
ủng hộ nha mọi người
trên thế giới này tui ghét nhất cái câu ôi thần linh ơi, mỗi khi con phim ấn độ nhất là cô dâu 8 tuổi nghe cái câu đó tắt tv nghỉ coi luôn


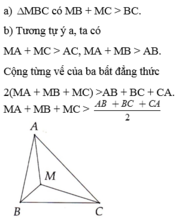
a) Xét ΔBMC ta có: MB + MC > BC (bất đẳng thức tam giác)
b)
*Xét ΔABM ta có: AM + BM > AB (1)
*Xét ΔACM ta có: AM + CM > AC (2)
*Xét ΔBMC ta có: BM + CM > BC (3)
Từ (1); (2); (3)
=> AM + BM + AM + CM + BM + CM > AB + AC + BC
=> 2. AM + 2. BM + 2. CM > AB + AC + BC
=> 2. (AM + BM + CM) > AB + AC + BC
Hay: 2. (MA + MB + MC) > AB + BC + CA
c)Gọi I là giao điểm của BM và AC.
Áp dụng bất đẳng thức tam giác vào ΔIMC ta có: MC<MI+IC (1)
Cộng MB vào hai vế (1) ta được: MC+MB<MI+IC+MB
⇒MC+MB<MI+MB+IC
⇒MC+MB<IB+IC (2)
d)Áp dụng bất đẳng thức tam giác vào ΔIBA ta có: IB<IA+AB (3)
Cộng IC vào hai vế (3) ta được: IB+IC<IA+AB+IC
⇒ IB+IC<IA+IC+AB
⇒IB+IC<AC+AB (4)
e)Từ (2) và (4) suy ra MB+MC<AB+AC
f)Áp dụng bđt tam giác, ta có:
AB+AI > BI = MB+MI, CI + MI > MC
=> AB + AI + CI + MI > MB + MI + MC
Mà AI + CI = AC
=> AB + AC > MB + MC [1]
Áp dụng bđt tam giác, ta cũng có:
BA + BC > MA + MC [2],
CA + CB > MA + MB [3]
Từ [1][2][3] => 2 (AB+AC+CA) > MA + MB + MC
=> MA + MB + MC < AB + AC + BC (đpcm)
chắc là đ
mong các pạn ủng hộ cho mk