Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

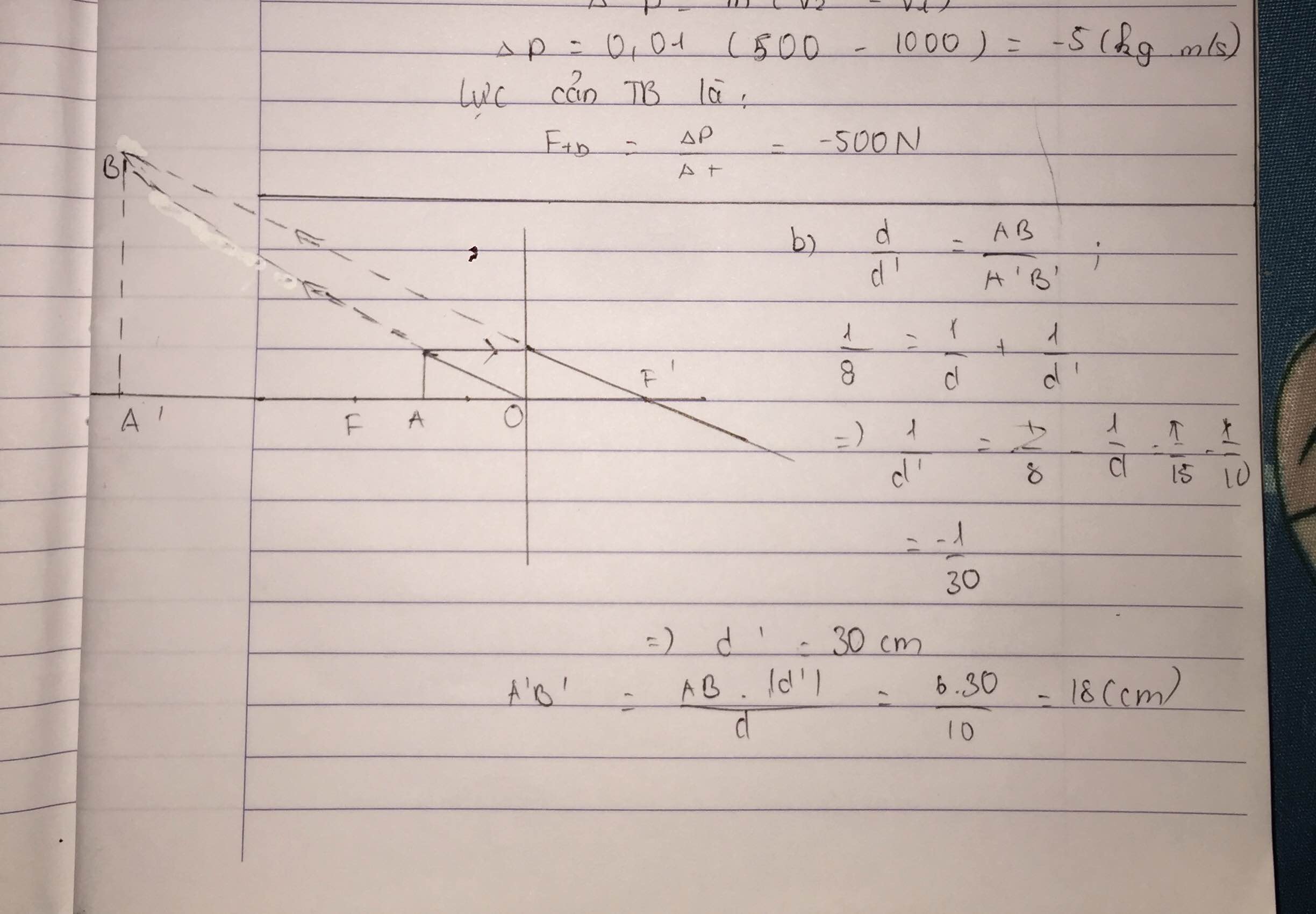
Khoảng cách từ ảnh đến thấu kính là:
Áp dụng công thức tính thấu kính:
\(\dfrac{1}{f}=\dfrac{1}{d}+\dfrac{1}{d'}\Rightarrow d'=\dfrac{d.f}{d-f}=\dfrac{8.4}{8-4}=8\left(cm\right)\)
Chiều cao của ảnh:
Ta có: \(\dfrac{d}{d'}=\dfrac{h}{h'}\Rightarrow h'=\dfrac{d'.h}{d}=\dfrac{8.2}{8}=2\left(cm\right)\)

a)Ảnh ảo, cùng chiều vật và nhỏ hơn vật.
b)Khỏang cách từ ảnh đến thấu kính:
\(\dfrac{1}{f}=\dfrac{1}{d'}-\dfrac{1}{d}\Rightarrow\dfrac{1}{36}=\dfrac{1}{d'}-\dfrac{1}{12}\)
\(\Rightarrow d'=9cm\)
Độ cao ảnh: \(\dfrac{h}{h'}=\dfrac{d}{d'}\)
\(\Rightarrow\dfrac{3}{h'}=\dfrac{12}{9}\Rightarrow h'=2,25cm\)

Ảnh thật, nhỏ hơn vật, cùng chiều với vật.
Nơi có ảnh cách thấu kính một đoạn:
\(\dfrac{1}{f}=\dfrac{1}{d}+\dfrac{1}{d'}\Rightarrow\dfrac{1}{20}=\dfrac{1}{60}+\dfrac{1}{d'}\)
\(\Rightarrow d'=30cm\)
Độ lớn ảnh:
\(\dfrac{h}{h'}=\dfrac{d}{d'}\Rightarrow\dfrac{4}{h'}=\dfrac{60}{30}\Rightarrow h'=2cm\)

Ảnh thật ngược chiều nhỏ hơn vật
\(\dfrac{1}{f}=\dfrac{1}{d}=\dfrac{1}{d'}\\\Leftrightarrow\dfrac{1}{4}=\dfrac{1}{6}+\dfrac{1}{d'}\\ \Rightarrow d'=12\)